Calculations with Excel

Two properties of spreadsheets result in a huge time-savings when doing calculations:

• the ability to copy formulas. This capability allows one to apply the same equations to an entire series of numbers.
• special functions provided by the spreadsheet program. There are literally hundreds of these special functions, including many that are valuable in statistics

The following problem was given in another tutorial (on calibration). I will be using it to illustrate just a few of Excel's capabilities. You can download an Excel 97 file with this data by clicking here.

Example

The following data was obtained in the analysis of copper using flame atomic absorption spectroscopy.

Following calibration, a sample of unknown copper concentration was analyzed. The measured transmittance was 35.6%. Report the concentration of analyte in the form of a confidence interval.

We need to calculate the absorbance of each calibration sample, since (as stated by Beer's Law), it is the absorbance (not the transmittance) that is linearly proportional to the analyte concentration. First type in the formula in the proper cell: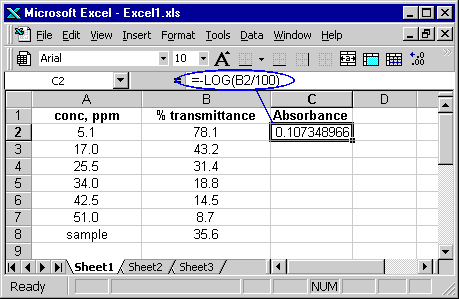

Next you can copy this formula so that the absorbance is calculated for all of the solutions. Use the Copy command in the "Edit" menu (or press Ctrl-C):

After copying, you will see a "marquee" surrounding the source cell. Select the desination cells using the mouse, and then use the Paste command in the "Edit" menu.

After the formula has been copied, the screen should look like this.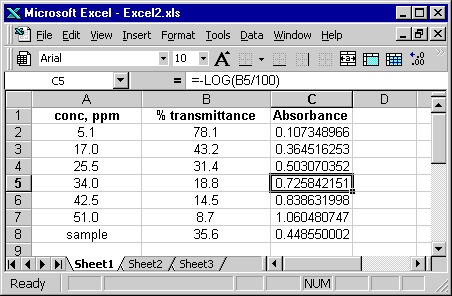

QuickTime movie showing the sequence of events to do these calculations. (click on the above image to download the Excel file)

This process is much faster than re-calculating the absorbance for every single solution and then typing it in. And it is just as fast with 100 numbers as with 5.

Two useful Excel functions are slope() and intercept(), which can be used to calculate the (you guessed it) the slope and intercept of a least-squares best-fit line through the data. Each function accepts two arguments, both of which are are range of cells: the Y-block and the X-block cells. Thus, for example, to calculate the slope, you type in "=slope(y-block, x-block)", where y-block and x-block are the range of the cells for the absorbance and concentration, respectively. Here is a screen shot after the functions have been applied.

See how to calculate slope and intercept of least-squares line using Excel formulas. (click the above image to download Excel file)

Excel provides many useful functions like slope() and intercept(). If you forget the name of a particular function, you can browse through the help file to find it.

Now that we know the intercept and slope of the least-squares best-fit line, we can actually calculate the values of that line for each solution (the "y-hat" value) using another formula. These calculated values are point estimates of the true absorbance of each solution. You can calculate the first value easily enough, as shown in the next screen-shot.

As expected, the best-fit value (0.109) is fairly close to the value actually measured (0.107). There is a problem, however, when this formula is copied to calculate the best-fit values for the other solutions, as shown in the next screen shot.

The best-fit values for every solution other than the first one are way off! The reason is that copying the equation as it was causes the cells that refer to the slope and intercept values to change (look carefully at the cell formula in the above figure). We want to change the formula so that the cells that refer to the intercept and slope are fixed (ie, what Excel calls absolute cell addresses) rather than variable (relative cell addresses). You can use the dollar signs ('$') to tell Excel not to change certain parts of a cell address. When composing the formula, the "F4" function key will toggle between various types of absolute and relative addresses.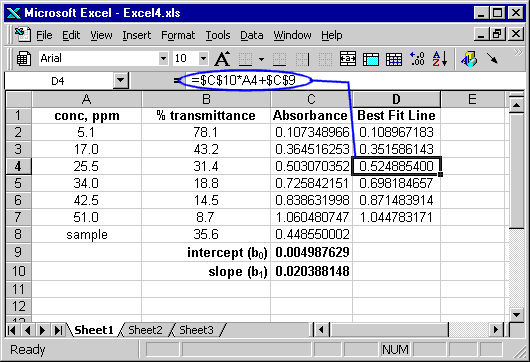

Sequence of events leading to the above screenshot (click the above image to download Excel file).

Finally, we can use this spreadsheet to answer the question originally posed: what is the copper concentration in the sample solution?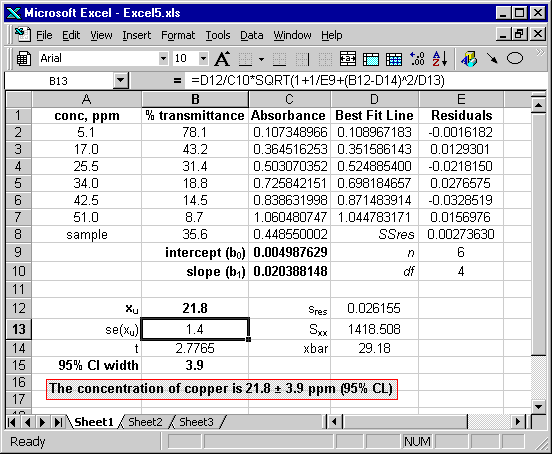

See how to obtain the screen shown above (you can click the above image to download Excel file).

Note that there is a faster way to calculate the standard deviation of the residuals (s_res) than the one shown here; I show you how in a later tutorial.