Ovidiu Lipan research lab
Is the future biology Shakespearean or Newtonian?
![]() Cells do not care about mathematics
Cells do not care about mathematics![]() thus concluded a biologist
friend after a discussion on the future of biology. And indeed, why should they
care? But if we exchange the word
thus concluded a biologist
friend after a discussion on the future of biology. And indeed, why should they
care? But if we exchange the word ![]() cell
cell![]() with
with ![]() rock
rock![]() ,
, ![]() Moon
Moon![]() or
or ![]() electrons
electrons![]() , do we have to change the sentence also? Why
should the Moon care about mathematics? We know however, that the Moon
navigates around the Earth on a mathematical orbit. If we think of how
electrons are described in Quantum Electrodynamics, then we can say that
electrons have a special taste for sophisticated mathematics. Today, life
scientists and computational scientists are engaged in many discussions of this
type. In short, the main theme of discussion is actually a question: Is the
future biology Shakespearean or Newtonian?
, do we have to change the sentence also? Why
should the Moon care about mathematics? We know however, that the Moon
navigates around the Earth on a mathematical orbit. If we think of how
electrons are described in Quantum Electrodynamics, then we can say that
electrons have a special taste for sophisticated mathematics. Today, life
scientists and computational scientists are engaged in many discussions of this
type. In short, the main theme of discussion is actually a question: Is the
future biology Shakespearean or Newtonian?
Although far from perfect, a Shakespearean play may serve as an analogy of how biological phenomena were described, studied and understood until very recently. Each character from Romeo and Juliet, for example, can be envisioned to be a molecule which plays a role in a complex cellular process. By studying the process experimentally, we hope to identify the characters in the play and to observe how they interact as the process proceeds. In the end we can describe the complex process just as the text of the play prescribes, for each scene, what each character is supposed to say and how to interact with the other characters on the stage.
However, formatting the biological knowledge in a Shakespeare-like drama is no longer enough. Like in physics or chemistry, the scientific drama must be sustained and accompanied by mathematical equations. The quantitative relations between players are as important as the players themselves. For example, a resistor is very important, but Ohm's law is important as well. The palpable resistor and the abstract Ohm's law cannot be separated if we want to understand an electric circuit. Therefore, the aim of biological research should be twofold: (1) to find the functional molecules that play a role in biochemical pathways and (2) to describe mathematically the interactions among these molecules and to understand the consequences of these interactions.
While much recent progress has been made towards (1) under the rubric of genome research, the study on (2) is still in its infancy. The emerging field of Systems Biology was borne with the (Newtonian) belief that biology can be described and understood in a mathematical language. In our analogy, a Newtonian science is not necessarily a deterministic science; in a broader sense, it is a science that recognizes that the book of Nature is written in a mathematical language, as Plato and Galileo stated long ago. What is the nature of this language for life sciences? And what might be a plausible path towards the Newtonian future for biology? (More details at paper11.pdf)
A mathematical law for heat stressed mammalian cells
The structure of an unknown biological system is uncovered by experimentally perturbing the system with a series of input signals. The response to these perturbations are measured as output signals. Then the mathematical relation between the input and the output signals constitutes a model for the system. As a result, a classification of biological molecular networks can be devised using their input-output functional relation. This article studies the input-output functional form for the response to heat shocks in mammalian cells. The Chinese-hamster ovary (CHO) mammalian cells were perturbed with a series of heat pulses of precise duration and temperature. The experimental data, taken at single-cell level, revealed a simple and precise mathematical law for the time evolution of the heat shock response. The parameters of the mathematical law can be experimentally measured and can be used by heat shock biologists to classify the heat shock response in different experimental conditions. Since the response to heat shock is the outcome of a transcriptional factor control, it is highly probable that the empirical law is valid for other biological systems. The mathematical model explains not only the mean value of the response but also the time evolution of its probability distribution in a cell population. (More details at paper12.pdf)

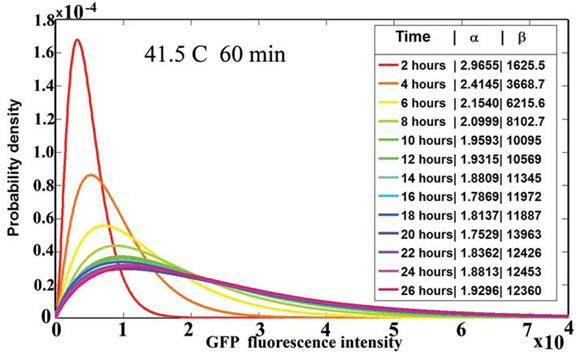
The use of oscillatory signals in the study of genetic networks
The structure of a genetic network is uncovered by studying its response to external stimuli (input signals). We present a theory of propagation of an input signal through a linear stochastic genetic network. We found that there are important advantages in using oscillatory signals over step or impulse signals and that the system may enter into a pure fluctuation resonance for a specific input frequency. (More details at paper09.pdf)
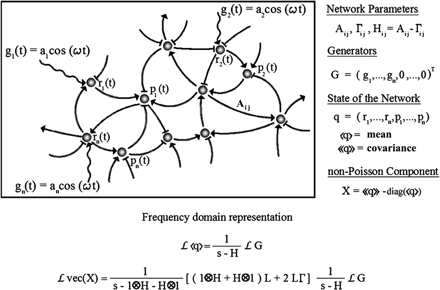
Figure: Response of a stochastic genetic network to an oscillatory input. The Laplace transform L changes the dynamic variable from time to frequency. In the vec(X) all of the elements of matrix X are arranged in a column vector.