Bayes's Theorem and the Likelihood Function

Over the past five years or so, a bunch of data have poured in that bear on the value of $\Omega$. They can be crudely summarized by saying that $\Omega$ has been measured to be

$$\Omega = 1.02 \pm 0.02.$$

What this means, roughly, is that the likelihood function looks like a bell curve with a peak at 1.02 and a width (standard deviation) of 0.02, roughly as shown in Figure 2.

Figure 2: Likelihood function. (This isn't normalized properly: the scale on the vertical axis is arbitrary.)

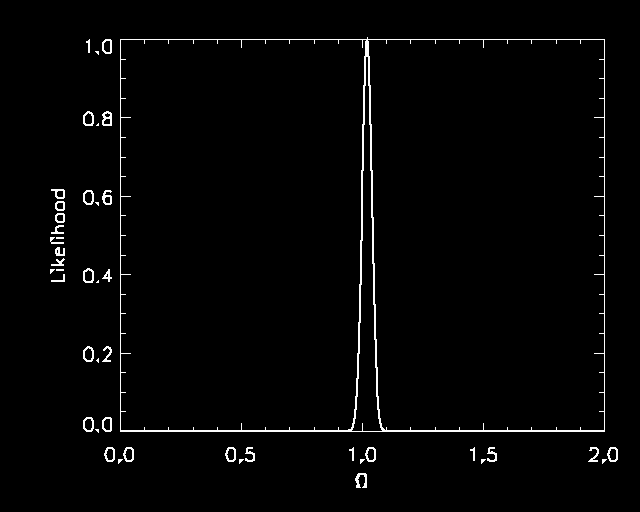
The likelihood function, by definition, is the probability density of getting the data that we actually observed, as a function of the value of $\Omega$. In other words, when we say that the likelihood function peaks at $\Omega=1.02$, we mean that this value of $\Omega$ is the best fit to the data. In a Universe with $\Omega=1.02$, the data that we actually observed are quite plausible. In a Universe with $\Omega =0.9$ (where the likelihood is extremely small), the data that we actually observed would have been quite unlikely to occur.

Now we're ready to state Bayes's theorem and apply it to the situation at hand. Bayes's theorem says that the posterior probability density is the product of the prior probability density and the likelihood function (times a constant):

$$\mbox{Posterior} \propto \mbox{Prior}\times\mbox{Likelihood}.$$

The constant of proportionality is chosen to make the posterior probability density integrate to 1.

If we take the prior shown in Figure 1 and multiply it by the likelihood function shown in Figure 2, we get the posterior probability density shown in Figure 3. Over the relatively small range of $\Omega$'s where the likelihood function was significantly different from zero (say 0.94-1.10 or so), the prior was essentially a constant plus that narrow delta-function spike at $\Omega =1$. That means that the posterior probability will be just a bump shaped like the likelihood function plus a delta-function spike as shown.

Figure 3: My posterior probability density. The narrow spike is a delta-function (infinitely high and narrow, with a finite area). For the choice of prior shown in Fig. 1, 99.5% of the area of this curve lies in the delta-function, and only 0.5% is in the broader bell curve.

You can work out what fraction of the total probability (that is, of the integral of the probability density) lies under the delta-function spike. For the prior shown in Figure 1, the answer turns out to be 99.5%. In other words, the data changed me from a 15% believer in $\Omega =1$ to someone who things there are 200-to-1 odds in favor of $\Omega =1$.

It's perhaps of interest to know how much those numbers depend on the details of the prior. Let's assume that a person's prior consists of a delta-function spike at $\Omega =1$, plus some smooth function of $\Omega$, and let's assume that the smooth bit can be taken to be constant in the region where the likelihood is significant (i.e., within a few standard deviations of $\Omega=1.02$). Then the prior can be characterized by two numbers: $p_i$, the prior probability of inflation (the area under the narrow spike at $\Omega =1$) and $\beta$, the ``background'' level in the vicinity. For example, my prior as shown in Figure 1 is characterized by $p_i$ =0.15 and $\beta$=0.01.

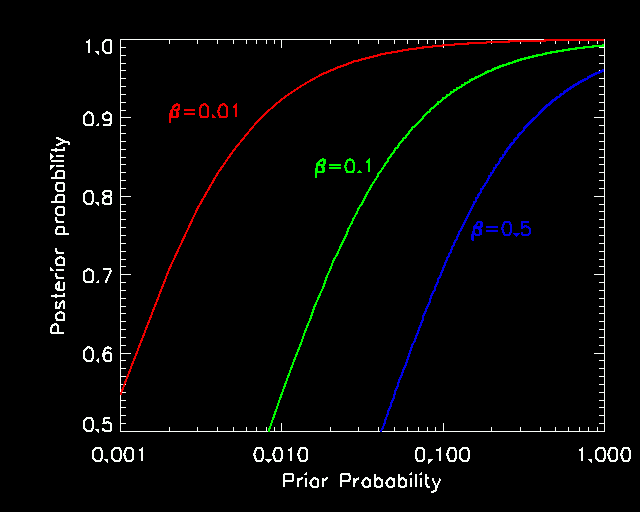
Figure 4 shows the posterior probability that $\Omega =1$ as a function of $p_i$ (the prior probability that $\Omega =1$), for a few different values of $\beta$. I would argue that $\beta=0.5$ is about as large as one would be likely to find.²

Figure 4: Posterior probability that $\Omega =1$, as a function of the prior probability. The parameter $\beta$ is the ``background level'' of the prior in the vicinity of $\Omega =1$.

This shows that, quite generically, people who thought there was any significant probability of $\Omega =1$ before the recent data rolled in should by now have very high assessments of the probability that $\Omega =1$.

Unless, of course, one simply disbelieves the data. The recent data come from several different experiments, using different techniques and probing different aspects of the Universe, and they all agree with each other. For that reason, I think that the current data are quite robust. Anyway, my purpose at the moment is not to convince you that you should believe the data, but simply to show how the posterior probabilities come out if you do believe the data.