My Prior

Figure 1 shows a cartoonish representation of my own personal prior probability density for $\Omega$, circa 1998. In case you don't know, the ``units'' of a probability density are probability per unit value of the parameter. The integral of the probability density from $a$ to $b$ gives the probability that the parameter's true value is in the interval from $a$ to $b$. The probability density must integrate to 1 over the entire possible range of parameters (which is 0 to infinity for $\Omega$).

Figure 1: My prior probability density. The narrow spike is a delta-function (infinitely high and narrow, with a finite area).

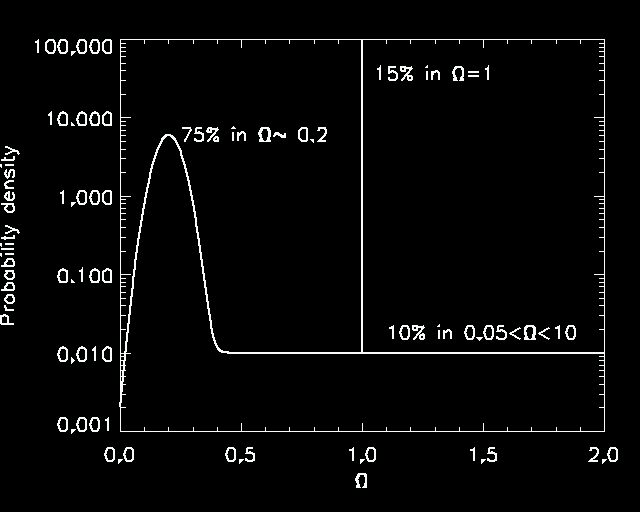
At that time, as I recall, I was fairly skeptical about inflation (compared to many other cosmologists). I estimate that at the time I thought there was about a 15% chance that inflation happened. That means that 15% of the total integral lies in a narrow (delta-function-like) spike at $\Omega =1$.

At that time, the balance of other evidence (leaving aside arguments in favor of inflation) tended to suggest that in fact $\Omega$ was about 0.2 with large uncertainties. That's why my prior has a large bump at $\Omega = 0.2$.

But the possibility was wide open that we were missing something important in our observation or interpretation of the data, so there was a finite probability that neither of the above possibilities was right. In that case, $\Omega$ could be just about anything. That's the reason for the flat portion of the probability density.

Let me emphasize that the details of this plot are very imprecise: I just cobbled together a crude model of what I think my opinions were at the time. The qualitative features are about right, but the exact values of the two key features that are going to matter later, namely the amount of probability in the $\Omega =1$ spike and the more-or-less flat background in the neighborhood of $\Omega =1$, could be significantly different.