To investigate quantum mechanical tunneling one
must extract the transmission coefficient from the
solution to the one-dimensional,
time-independent Schrödinger equation.
The transmission coefficient is the ratio of
the flux of particles that penetrate a potential barrier to
the flux of particles incident on the barrier.
It is related to the probability that tunneling will occur.
Consider a rectangular
potential barrier of height V0 as shown in Figure 1.
The general solution of the Schrödinger equation in each region is
where
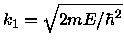 and
and
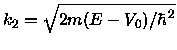 .
This solution can be rewritten as a vector dot product so, for
example, in Region 2 of Figure 1
.
This solution can be rewritten as a vector dot product so, for
example, in Region 2 of Figure 1
 |
(5) |
where the 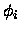 are the coefficient vectors
representing the wave function in each region.
To generate relationships among the coefficients
in Equations 2-4 one requires
the wave function and its first derivative to be continuous
at the boundaries of each region in Figure 1.
At x=0 this leads to two expressions.
are the coefficient vectors
representing the wave function in each region.
To generate relationships among the coefficients
in Equations 2-4 one requires
the wave function and its first derivative to be continuous
at the boundaries of each region in Figure 1.
At x=0 this leads to two expressions.
| A+B |
= |
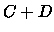 |
(6) |
| i k1A - i k1 B |
= |
i k2 C - i k2 D |
(7) |
In matrix notation Equations 6-7 can be expressed in the following way.
Using the definition of the matrix inverse yields the following result
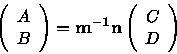 |
(10) |
which can be expressed as
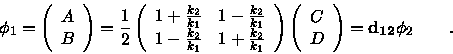 |
(11) |
The matrix,
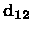 ,
is known as the discontinuity
matrix and `connects' the coefficient vectors
,
is known as the discontinuity
matrix and `connects' the coefficient vectors 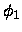 and
and
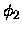 in Region 1 and
Region 2.
in Region 1 and
Region 2.
The wave function and its derivative must also be
continuous at
x=a.
At this point, consider a new coordinate system
such that the
transition from Region 2 to Region 3 takes place at
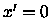 .
By analogy with Equation 11 one can show that,
.
By analogy with Equation 11 one can show that,
 |
(12) |
where the
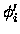 are the coefficient vectors in the
new coordinate system in the equivalent regions of the
potential energy curve and
are the coefficient vectors in the
new coordinate system in the equivalent regions of the
potential energy curve and
 has the same form as
has the same form as
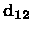 in Equation 3 except for the interchange of the
indices.
To exploit this result, one must relate the
coefficient vectors in the
primed coordinate system to the ones in the original
coordinates.
The original coordinate system is transformed such
that
in Equation 3 except for the interchange of the
indices.
To exploit this result, one must relate the
coefficient vectors in the
primed coordinate system to the ones in the original
coordinates.
The original coordinate system is transformed such
that
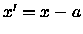 .
The new wave function in Region 2 must satisfy
.
The new wave function in Region 2 must satisfy
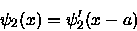 |
(13) |
which can be written in matrix form and rearranged to yield the following
result (recall Equation 5).
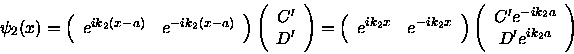 |
(14) |
The row vector on the right hand side of Equation 14 is
the same as the row vector in Equation 5 so
the coefficient
vectors representing  and
and
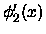 are
related
by
are
related
by
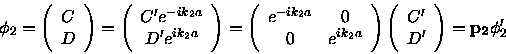 |
(15) |
where 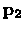 is the propagation matrix in Region 2.
Similarly, one can show that
is the propagation matrix in Region 2.
Similarly, one can show that
 |
(16) |
where
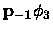 shifts the wave function back to the original
coordinate system.
Combining Equations 11,12, 15, and 16 and setting G=0 since there
are no incoming waves in Region 3 one obtains
shifts the wave function back to the original
coordinate system.
Combining Equations 11,12, 15, and 16 and setting G=0 since there
are no incoming waves in Region 3 one obtains
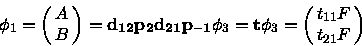 |
(17) |
where  is the transfer matrix relating the
coefficient vectors in Regions 1 and 3.
The transmission
coefficient is then
is the transfer matrix relating the
coefficient vectors in Regions 1 and 3.
The transmission
coefficient is then
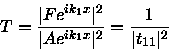 |
(18) |
This treatment of the rectangular
potential barrier problem can be extended to potential barriers
of arbitrary shape.
Consider the radioactive  -decay of
-decay of
 .
The potential barrier is shown as the solid curve in Figure 2.
.
The potential barrier is shown as the solid curve in Figure 2.
Figure:
50pt
50pt
Potential energy curve for an  particle in
the force field of
particle in
the force field of
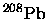 ,
the daughter nucleus of the
,
the daughter nucleus of the
 decay.
decay.
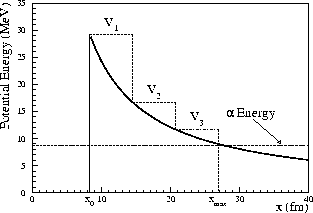 |
The central portion of the curve is the Coulomb
potential
V(x) = Z1 Z2 e2/x where x is the distance between the
nuclear centers and the product of the charges is
Z1 Z2 e2.
It is divided into a sequence of adjacent
barriers (the dot-dashed lines)lying between the
nuclear radius, x0, and the classical turning point,
xmax, for an
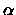 particle of total energy, E.
The potential energy is taken to be zero outside
these limits in the manner of Condon and Gurney.12
One can now
use the propagation and discontinuity matrices to relate the wave
function inside the barrier to the wave function outside
(x>xmax).
For the configuration shown in Figure 2 one chooses the origin at the
nuclear radius and the two wave
functions are related by
particle of total energy, E.
The potential energy is taken to be zero outside
these limits in the manner of Condon and Gurney.12
One can now
use the propagation and discontinuity matrices to relate the wave
function inside the barrier to the wave function outside
(x>xmax).
For the configuration shown in Figure 2 one chooses the origin at the
nuclear radius and the two wave
functions are related by
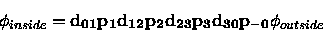 |
(19) |
where
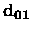 is the discontinuity matrix between the
region where V(x) = 0 and
V(x) = V1,
is the discontinuity matrix between the
region where V(x) = 0 and
V(x) = V1,  is the
propagation matrix where
V(x) = V1, and so on.
The propagation matrix
is the
propagation matrix where
V(x) = V1, and so on.
The propagation matrix
 returns the wave function to the
appropriate coordinate system.
The last matrix
returns the wave function to the
appropriate coordinate system.
The last matrix
 is unnecessary for calculating the
transmission coefficient since it changes the coordinates, but
does not change the ratio of the coefficients.
The adequacy of treating the potential energy curve in Figure
2 as a sequence of adjacent rectangular barriers will improve
as the number of barriers increases and should converge to
some limiting value.
The transmission coefficient will be extracted from the
transfer matrix using Equation 18.
is unnecessary for calculating the
transmission coefficient since it changes the coordinates, but
does not change the ratio of the coefficients.
The adequacy of treating the potential energy curve in Figure
2 as a sequence of adjacent rectangular barriers will improve
as the number of barriers increases and should converge to
some limiting value.
The transmission coefficient will be extracted from the
transfer matrix using Equation 18.
1998-09-14
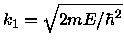 and
and
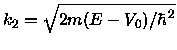 .
This solution can be rewritten as a vector dot product so, for
example, in Region 2 of Figure 1
.
This solution can be rewritten as a vector dot product so, for
example, in Region 2 of Figure 1
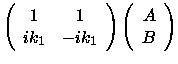
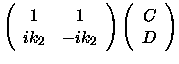
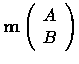
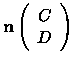
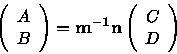
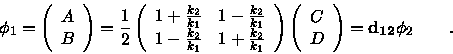
![]() .
By analogy with Equation 11 one can show that,
.
By analogy with Equation 11 one can show that,
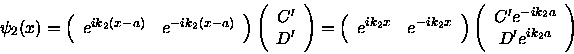
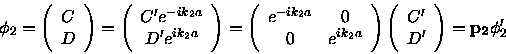
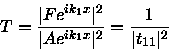
![]() -decay of
-decay of
![]() .
The potential barrier is shown as the solid curve in Figure 2.
.
The potential barrier is shown as the solid curve in Figure 2.
