A New Teaching Approach

To Quantum Mechanical Tunneling

G.P.Gilfoyle
Physics Department
University of Richmond, Virginia
ggilfoyl@richmond.edu

Outline

1.

Background and motivation.

2.

The transfer matrix approach to tunneling.

3.

Application to radioactive decay.

4.

Classroom results.

5.

Conclusions.

Background and Motivation

1.

Why bother?

• Use computational tools.
• Use a `hands-on' laboratory approach.

2.

The Program

• Present the observations.
• Build a model.
• Use the tools.
• Use this program regularly.

3.

Is it physically rigorous?

• Advantages over WKB and finite difference methods.

4.

Did it work?

• Easy, consistent, engaging method of investigating quantum mechanics.

Solving the Schrödinger Equation

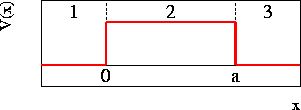
The one-dimensional, nonrelativistic Schrödinger equation is

$${-\hbar^2 \over 2m} {\partial^2 \psi(x) \over \partial x^2} + V(x)\psi(x) = E\psi(x) \qquad .$$

The general solution is

$$\begin{eqnarray*}\psi_1 (x) &=& A e^{ik_1 x} + B e^{-ik_1x} \quad (x< 0) \\ \... ...) \\ \psi_3 (x) &=& F e^{ik_1 x} + G e^{-ik_1x} \quad (a < x) \end{eqnarray*}$$

$${\rm where} \qquad \hfil k_1 = \sqrt{2mE/\hbar^2} \qquad k_2 = \sqrt{2m(E-V_0)/\hbar^2} \quad .$$

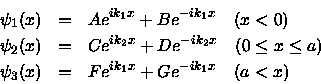
Express this solution as a matrix.

$$\psi_1 (x) = \pmatrix{ e^{ik_1x} & e^{-ik_1x} \cr} \pmatrix{ A \cr B \cr } = \pmatrix{ e^{ik_1x} & e^{-ik_1x} \cr} \phi_1$$

$$\psi_2 (x) = \pmatrix{ e^{ik_2x} & e^{-ik_2x} \cr} \pmatrix{ C \cr D \cr } = \pmatrix{ e^{ik_2x} & e^{-ik_2x} \cr} \phi_2$$

$$\psi_3 (x) = \pmatrix{ e^{ik_1x} & e^{-ik_1x} \cr} \pmatrix{ F \cr G \cr } = \pmatrix{ e^{ik_2x} & e^{-ik_2x} \cr} \phi_3$$

Get the Particular Solution

Match the wave function and its derivative at the boundaries.

$$\begin{eqnarray*}A+B &=& C+D \hfil \\ i k_1A - i k_1 B &=& i k_2 C - i k_2 D \end{eqnarray*}$$

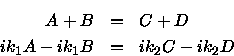
Write the result in matrix form.

$$\begin{eqnarray*}\left ( \begin{array}{cc} 1 & 1 \\ ik_1 & -ik_1 \end{array}... ...{\bf n} \left ( \begin{array}{c} C\\ D \end{array} \right ) \end{eqnarray*}$$

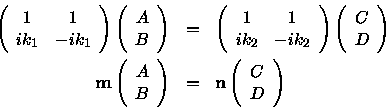
Use the definition of the matrix inverse and get

$$\begin{array}{c} \left ( \begin{array}{c} A\\ B \end{arr... ...( \begin{array}{c} C\\ D \end{array} \right ) \end{array}$$

which can be expressed in matrix form as

$$\phi_1 = \left ( \begin{array}{c} A\\ B \end{array} \right ) ... ...c} C \\ D \end{array} \right ) = {\bf d_{12}} \phi_2 \qquad .$$

The discontinuity matrix!

Make Things Simple

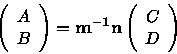
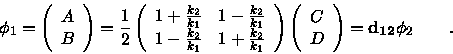
Shift coordinates.

Match the wave function and its derivative at the right-hand-side boundary in the new coordinates.

$$\phi^\prime_2 = {\bf d_{21}} \phi^\prime_3$$

Relate the two coordinate systems.

$$\begin{eqnarray*}x^\prime &=& x - a \\ \psi_2(x) &=& \psi^\prime_2(x-a) \end{eqnarray*}$$

And obtain the following result.

$$\phi_2 = \left ( \begin{array}{c}C\\ D \end{array} \right ) ... ...ime \\ D^\prime \end{array} \right ) = {\bf p_2}\phi_2^\prime$$

The propagation matrix!

Pull Things Together

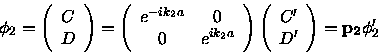
Build the transfer matrix

$$\begin{eqnarray*}\phi_1 &=& {\bf d_{12}} \phi_2 \\ &=& {\bf d_{12}} \left ( {\... ...left ( {\bf p_{-1}} \phi_3 \right ) \qquad \qquad \qquad \qquad \end{eqnarray*}$$

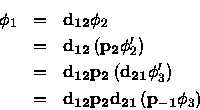
The final result.

$$\begin{eqnarray*}\phi_1 &=& {\bf d_{12}} {\bf p_2} {\bf d_{21}} {\bf p_{-1}} \ph... ... \pmatrix{ A \cr B \cr} &=& \pmatrix{t_{11} F \cr t_{21} F \cr} \end{eqnarray*}$$

Get the transmission coefficient.

$$\begin{eqnarray*}T &=& {\rm Outgoing\ flux \over Incoming\ flux} \\ [15pt] &=& ... ... &=& {1 \over \vert t_{11}\vert^2} \qquad \qquad \qquad \qquad \end{eqnarray*}$$

Pull Things Together

Gather the pieces.

$$\phi_1 = {\bf d_{12}} \phi_2 \qquad \phi_2 = {\bf p_2}\phi_2^\prime \qquad \phi_2^\prime = {\bf d_{21}}\phi_3^\prime$$

Build the transfer matrix.

$$\begin{eqnarray*}\phi_1 &=& {\bf d_{12}} \phi_2 \\ &=& {\bf d_{12}} \left ( {\... ...left ( {\bf p_{-1}} \phi_3 \right ) \qquad \qquad \qquad \qquad \end{eqnarray*}$$

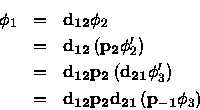
The final result.

$$\begin{eqnarray*}\phi_1 &=& {\bf d_{12}} {\bf p_2} {\bf d_{21}} {\bf p_{-1}} \ph... ... \pmatrix{ A \cr B \cr} &=& \pmatrix{t_{11} F \cr t_{21} F \cr} \end{eqnarray*}$$

Get the transmission coefficient.

$$T = {\rm Outgoing\ flux \over Incoming\ flux} = {\vert F e^... ... \vert A e^{i k_1 x}\vert^2} = {1 \over \vert t_{11}\vert^2}$$

Multiple Barriers

Consider a series of rectangular barriers.

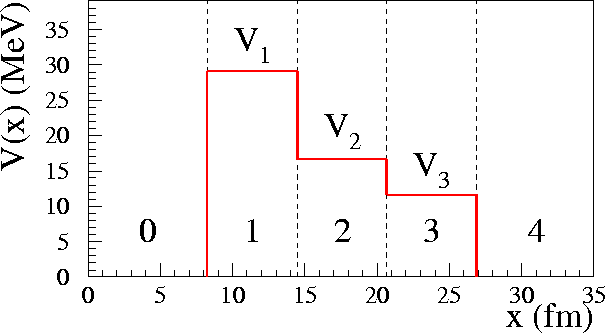
Build up the transfer matrix.

$$\begin{eqnarray*}\phi_{left} &=& {\bf d_{01} } {\bf p_1} {\bf d_{12}} {\bf p_2} ... ... \pmatrix{ A \cr B \cr} &=& \pmatrix{t_{11} F \cr t_{21} F \cr} \end{eqnarray*}$$

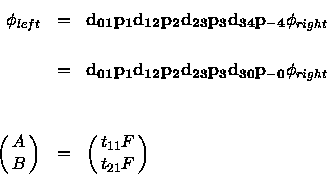
And get the transmission coefficient as before.

$$T = {1 \over \vert t_{11}\vert^2} \qquad \qquad \qquad \qquad \qquad$$

Programming the Algorithm
in Mathematica

Define a function to calculate the transmission coefficient.

RadDecay[Znuc_,Anuc_,Eout_,Ndiv_] := ( 

(* constants *)
   Mout  = Aout*AtoMeV;
   R0    = r0*(Anuc - Aout)^(1/3);
   Rmax  = Zout*(Znuc - Zout)*e2/Eout;
   step  = (Rmax - R0)/Ndiv;

(* table of barrier heights *)
   Ve    = Table[{r, Zout*Znuc*e2/r},{r, R0, Rmax-step,step}];
              
(* put zeros at each end of the array. *)
   PrependTo[Ve, {R0-step, 0}];
   AppendTo[Ve, {Rmax, 0}];

(* initialize the transfer matrix. *)
   trans = { {1,0}, 
             {0,1} };

(* loop over the barriers *)
   Do[
     V1  = Ve[[i,2]];
     V2  = Ve[[i+1,2]];
     k1  = Sqrt[2*Mout*(Eout - V1)/(hbarc^2) ];
     k2  = Sqrt[2*Mout(Eout - V2)/(hbarc^2) ];
     d   = 0.5*{ {1 + (k2/k1), 1 - (k2/k1)},
                 {1 - (k2/k1), 1 + (k2/k1)} };
     p   = { {E^(I*k2*step),             0}, 
             {0            ,E^(-I*k2*step)} };
     trans = trans.d.p;,
     {i,1,Ndiv+1}
 ];
 
(* get the transmission coefficient. *)  
   tr = Abs[1/(Conjugate[ trans[[1,1]] ]*trans[[1,1]])];
   Print["Transmission Coefficient: ",tr]
)

Comparison With Other Methods

1.

The WKB approximation.

• It does not reduce to the rectangular barrier correctly while the transfer matrix method does.

• The connection between the rectangular barrier and potentials of arbitrary shape is less transparent for the WKB than the transfer matrix method.

2.

Numerical integration of the Schrödinger equation.

• It can be more difficult than the transfer matrix method.

• It's less accessible to undergraduates. Students are unfamiliar with numerical methods, but are well acquainted with matrix operations.

Classroom Results

1.

The method is accessible.

• Undergraduates can do it.

• Matrix operations are familiar.

2.

The student response is good.

3.

It's broadly applicable.

• Used to study the rectangular barrier, $\alpha$-decay, and one-dimensional solids.

4.

Computational laboratories work.

• Students score in the $\rm 75^{th}$ percentile in the quantum mechanics portion of the Educational Testing Service's Field of Study physics test (1994-1997).

Conclusions

1.

Physically rigorous.

• More consistent than the WKB approximation.
• Broadly applicable.

2.

It's pedagogically appealing.

• It's accessible and engaging to undergraduates.
• Uses modern computational tools.

3.

Part of a successful program of incorporating a `hands-on' computational laboratory experience.

Support provided by the United States National Science Foundation and the University of Richmond.