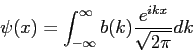
where the
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature:
Questions (6 pts. apiece) Answer questions in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions circle the correct answer.
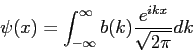
Problems. Clearly show all work for full credit.
| 1. (15 pts.) |
A 5.30-MeV |
| 2. (25 pts.) |
Recall our old friend, Newton's Second Law,
where |
| 3. (30 pts) |
Electrons in a beam of density
|
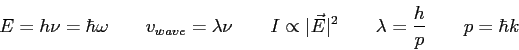
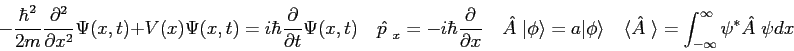
The wave function,
![]() , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
![]() and
and
![]() ) .
) .
![\begin{displaymath}
\psi_1 =
{\bf t} \psi_3 =
{\bf d_{12} p_2 d_{21} p_1^{-1...
..._{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img33.png)

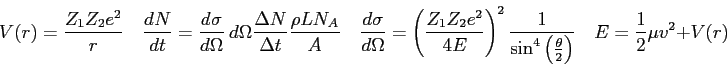
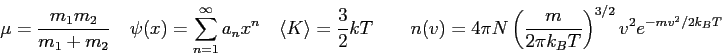
| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
||