| (a) | 7.87 fm | (d) | 10.64 fm |
| (b) | 15.74 fm | (e) | 13.20 fm |
| (c) | 5.32 fm |
where
| (a) | (d) | ||
| (b) | (e) | ||
| (c) |
| (a) |
|
(d) | |
| (b) |
|
(e) |
|
| (c) |
![\includegraphics[]{mp3.eps}](img84.png)
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Multiple Choice Questions (5 points apiece).
| (a) | 7.87 fm | (d) | 10.64 fm |
| (b) | 15.74 fm | (e) | 13.20 fm |
| (c) | 5.32 fm |
| (a) | (d) | ||
| (b) | (e) | ||
| (c) |
| (a) |
|
(d) | |
| (b) |
|
(e) |
|
| (c) |
![\includegraphics[]{mp3.eps}](img84.png)
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
Problems. Clearly show all work for full credit.
| 1. (20 pts.) | A harmonic oscillator with
energy
|
| 2. (20 pts.) | Calculate the expectation value of the momentum for
a particle in the 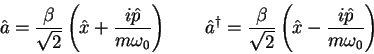
where |
| 3. (40 pts.) | In class we found the general solution to the
rectangular barrier
problem for the potential shown in the figure below.
This general solution in the three regions labelled in the figure is 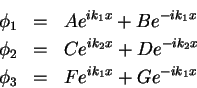
where the wave numbers are defined in the following way. 
|
| 3. (cont.) | We expressed the wave functions in
each region in the form of column vectors
and the boundary conditions in the form of the matrices where 
Consider the elements of
|
| Speed of light |
|
|
| Boltzmann's constant |
|
|
|
|
||
| Planck's constant |
|
|
|
|
||
|
|
||
|
|
||
|
|
||
| Electron charge |
|
|
| Electron mass |
|
|
| Proton mass |
|
|
| Neutron mass |
|
|
| atomic mass unit |
|
|
| Fine structure constant |