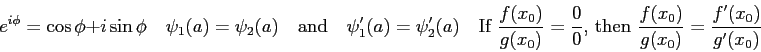Physics 309 Test 2
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (6 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided.
- Consider the set of data in the table. A theoretical prediction requires
these data to be constant.
In words, describe a procedure to determine quantitatively if the data agreed with that prediction.
Explain your reasoning.
| 0.59395 |
0.635293 |
| 0.523303 |
0.342906 |
| 0.638051 |
0.42535 |
| 0.4888 |
0.759856 |
| 0.381186 |
0.562729 |
- What is the paradox of the alpha decay of
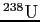 ?
?
- Let the potential energy of the NaCl molecule be
described by
where 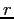 is the internuclear separation.
If the equilibrium separation is
is the internuclear separation.
If the equilibrium separation is
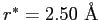 and the dissociation energy is
and the dissociation energy is
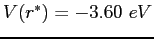 , then find the
constants
, then find the
constants 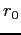 and
and 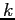 .
.
- (A.)
- (B.)
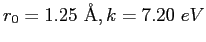
- (C.)

- (D.)
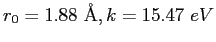
- (E.)

![\includegraphics[height=0.75in]{NaCl.eps}](img99.png)
- A particle of energy
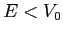 is incident on a step
potential of height
is incident on a step
potential of height 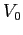 .
Let
.
Let
Find the transmission coefficient.
- 1
- 0
-
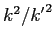
-
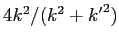
-
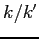
![\includegraphics[height=1.25in]{stepbarrier.eps}](img100.png)
- A deuteron (
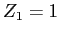 ,
,  ) is incident on a
lead nucleus (
) is incident on a
lead nucleus (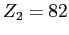 ,
, 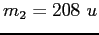 ) at the Brookhaven
National Laboratory.
The terminal voltage of the accelerator is
) at the Brookhaven
National Laboratory.
The terminal voltage of the accelerator is 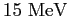 .
Find the distance of closest approach in a head-on collision.
.
Find the distance of closest approach in a head-on collision.
| (a) |
7.87 fm |
(d) |
10.64 fm |
| (b) |
15.74 fm |
(e) |
13.20 fm |
| (c) |
5.32 fm |
|
|
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
A mass 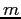 is oscillating freely on a vertical spring. When is oscillating freely on a vertical spring. When 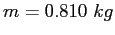 ,
the period is ,
the period is 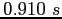 .
An unknown mass on the same spring has a period of .
An unknown mass on the same spring has a period of 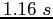 .
What is the spring constant .
What is the spring constant 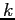 and the unknown mass? and the unknown mass?
|
| 2. (20 pts) |
Recall our old friends, Newton's Second Law,
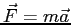 and Hooke's Law,
and Hooke's Law,
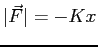 which can be combined to form a
differential equation which can be combined to form a
differential equation
where
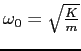 .
The solutions of this equation are well known, but now solve this differential
equation using the Method of Frobenius (i.e. the power series method) and
obtain the recursion relationship. .
The solutions of this equation are well known, but now solve this differential
equation using the Method of Frobenius (i.e. the power series method) and
obtain the recursion relationship.
|
width10cm height1pt depth0pt
Physics 309 Conversions, and Constants
Speed of light (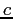 ) ) |
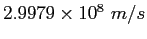 |
fermi (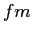 ) ) |
 |
Boltzmann constant (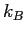 ) ) |
 |
angstrom (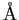 ) ) |
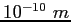 |
| |
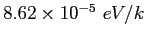 |
electron-volt (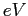 ) ) |
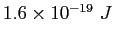 |
Planck constant (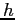 ) ) |
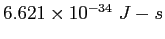 |
MeV |
 |
| |
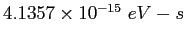 |
GeV |
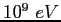 |
Planck constant (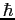 ) ) |
 |
Electron charge (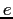 ) ) |
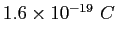 |
| |
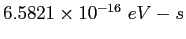 |
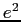 |
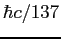 |
Planck constant ( ) ) |
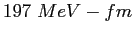 |
Electron mass ( ) ) |
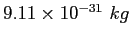 |
| |
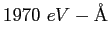 |
|
 |
Proton mass (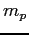 ) ) |
 |
atomic mass unit (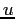 ) ) |
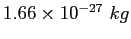 |
| |
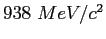 |
|
 |
Neutron mass (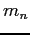 ) ) |
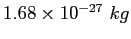 |
|
|
| |
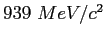 |
|
|
width10cm height1pt depth0pt
Physics 309 Equations
The wave function,
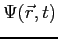 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 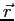 to
to
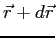 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
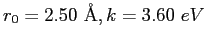
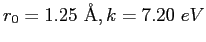

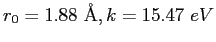

![\includegraphics[height=0.75in]{NaCl.eps}](img99.png)
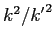
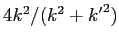
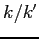
![\includegraphics[height=1.25in]{stepbarrier.eps}](img100.png)
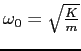 .
The solutions of this equation are well known, but now solve this differential
equation using the Method of Frobenius (i.e. the power series method) and
obtain the recursion relationship.
.
The solutions of this equation are well known, but now solve this differential
equation using the Method of Frobenius (i.e. the power series method) and
obtain the recursion relationship.
 . The eigenfunctions and eigenvalues for this particle in a box
are the following.
. The eigenfunctions and eigenvalues for this particle in a box
are the following.
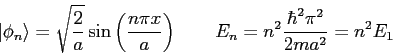
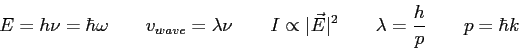
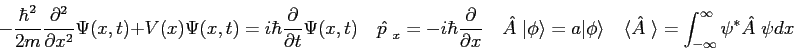

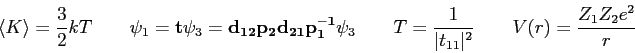
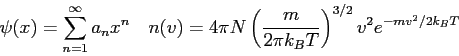

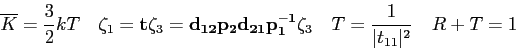
![\begin{displaymath}
T_{WKB} = \exp\left [ -2 \int_{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img96.png)