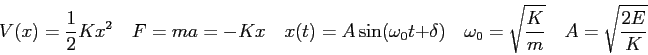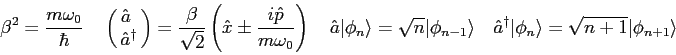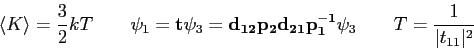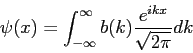 |
(1) |
| (2) |
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature:
Questions (5 pts. apiece) Answer questions in complete, well-written sentences WITHIN the spaces provided.
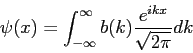 |
(1) |
| (2) |
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
Fusion reactions in the Sun are responsible for
the production of solar energy.
One of these reactions is the fusion of a proton with a
deuteron (a proton and neutron
bound together).
The deuteron has a radius of about |
| 2. (25 pts) |
Consider the following initial state for a particle in a box with walls at 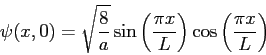
The eigenfunctions and eigenvalues are 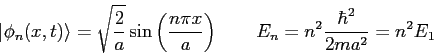
What is |
| 3. (30 pts) |
For a harmonic oscillator state in the superposition state at 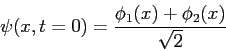
what is |
| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
||

The wave function,
![]() , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.