![\includegraphics[height=1.5in]{f1.eps}](img83.png)
Find the constant
| A. |
|
B. |
|
| C. | D. |
|
|
| E. |
| A. | D. |
|
|
| B. | E. |
|
|
| C. |
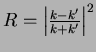 |
![\includegraphics[height=1.0in]{stepbarrier.eps}](img84.png)
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (5 pts. apiece) Answer questions 1-3 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 4-5 circle the correct answer.
![\includegraphics[height=1.5in]{f1.eps}](img83.png)
| A. |
|
B. |
|
| C. | D. |
|
|
| E. |
| A. | D. |
|
|
| B. | E. |
|
|
| C. |
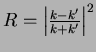 |
![\includegraphics[height=1.0in]{stepbarrier.eps}](img84.png)
Problems. Clearly show all work for full credit.
| 1. (25 pts.) |
A free particle of mass where 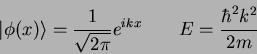
What is |
| 2. (25 pts) |
Recall our old friends, Newton's Second Law,
where |
| 3. (25 pts) |
An electron beam is incident on a barrier of height |
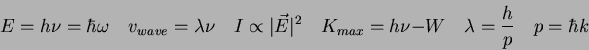
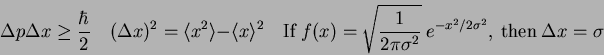
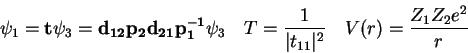
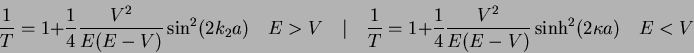
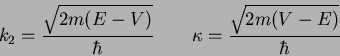
| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
||