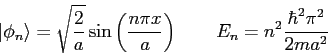
where
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature:
Questions (6 pts. apiece) Answer questions in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions circle the correct answer.
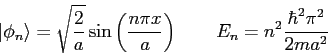
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
What is the de Broglie wavelength of a |
||||||
| 2. (20 pts.) |
What is the expectation value of the momentum
|
||||||
| 3. (30 pts) |
A pulse neutrons of length
The eigenfunctions and eigenvalues for the neutrons are the following.
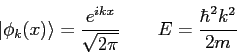
At |
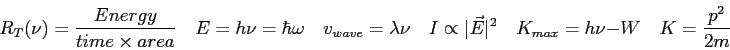

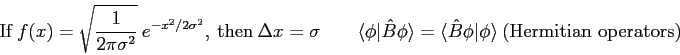
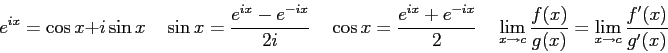
The wave function,
![]() , contains all we know of a system and
, contains all we know of a system and ![]() is the probability of finding it in
the region
is the probability of finding it in
the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
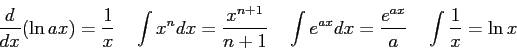
| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
||