| (a) | 2.76 eV | (d) | 4.76 eV |
| (b) | 2.29 eV | (e) | 1.00 eV |
| (c) | 0.47 eV |
![\includegraphics[]{f1.eps}](img84.png)
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
| (a) |
|
(d) |
|
| (b) |
|
(e) | |
| (e) |
|
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Multiple Choice Questions (5 points apiece).
| (a) | 2.76 eV | (d) | 4.76 eV |
| (b) | 2.29 eV | (e) | 1.00 eV |
| (c) | 0.47 eV |
![\includegraphics[]{f1.eps}](img84.png)
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
| (a) |
|
(d) |
|
| (b) |
|
(e) |
|
| (c) |
|
| (a) |
|
(d) |
|
| (b) |
|
(e) | |
| (e) |
|
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
A criterion which discerns if a given configuration is classical
or quantum mechanical may be stated in terms of the de Broglie
wavelength 
A rubidium atom of mass |
||||||
| 2. (20 pts.) |
Consider the functions below defined over the interval 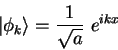
|
||||||
| 3. (40 pts.) |
Consider a case of one dimensional nuclear
`fusion'.
A neutron is in the potential well of a nucleus that we will
approximate with an infinite square well with
walls at 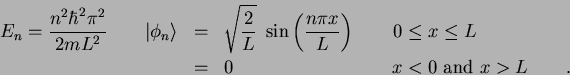
The neutron is in the
|
| Speed of light |
|
|
| Boltzmann's constant |
|
|
|
|
||
| Planck's constant |
|
|
|
|
||
|
|
||
|
|
||
|
|
||
| Electron charge |
|
|
| Electron mass |
|
|
| Proton mass |
|
|
| Neutron mass |
|
|
| atomic mass unit |
|
|
| fermi | ||
| angstrom | ||
| electron-volt |
|
|
| mega-electron-volt | ||
| giga-electron-volt | ||
| electron-charge squared |