where
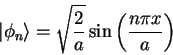
where
| A. | 4.50 eV | D. | 2.25 eV |
| B. | 3.60 eV | E. | 2.79 eV |
| C. | 7.29 eV |
| A. | D. | ||
| B. | E. | ||
| C. |
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (5 pts. apiece) Answer questions 1-3 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 4-5 circle the correct answer.
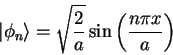
| A. | 4.50 eV | D. | 2.25 eV |
| B. | 3.60 eV | E. | 2.79 eV |
| C. | 7.29 eV |
| A. | D. | ||
| B. | E. | ||
| C. |
Problems. Clearly show all work for full credit.
| 1. (30 pts.) |
We developed in class the time-dependent form of the Schroedinger equation
shown below.
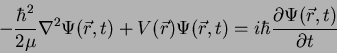
We now want to show that for the one-dimensional case and for potential energy functions that depend only on position (i.e., 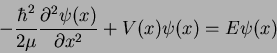
|
| 3. (45 pts) |
Ten million neutrons are in a one-dimensional box with walls
at where 
|
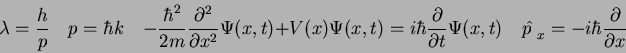

| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
||