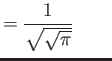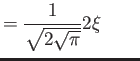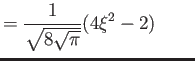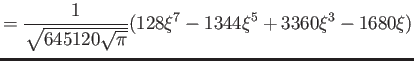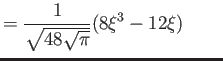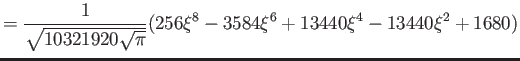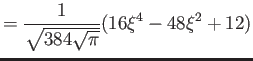Physics 309 Final
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Name height0pt depth1pt width2.5in Signature height0pt depth1pt width2.5in
Questions (3 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided.
- Recall the vibration-rotation spectrum of carbon monoxide shown in the figure.
If the
 molecule absorbed a photon to go from the
molecule absorbed a photon to go from the 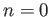 to
to 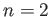 vibrational state where
would it appear on the plot below. Explain your reasoning.
vibrational state where
would it appear on the plot below. Explain your reasoning.
- For the
 vibrator-rotator what is the formula for the peaks above the
red line in the figure corresponding to the transition
vibrator-rotator what is the formula for the peaks above the
red line in the figure corresponding to the transition
 ,
,
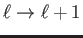 ?
Start from the expression for the
?
Start from the expression for the  energy levels and get your
result in terms of
energy levels and get your
result in terms of  ,
,
 , and any other constants.
, and any other constants.
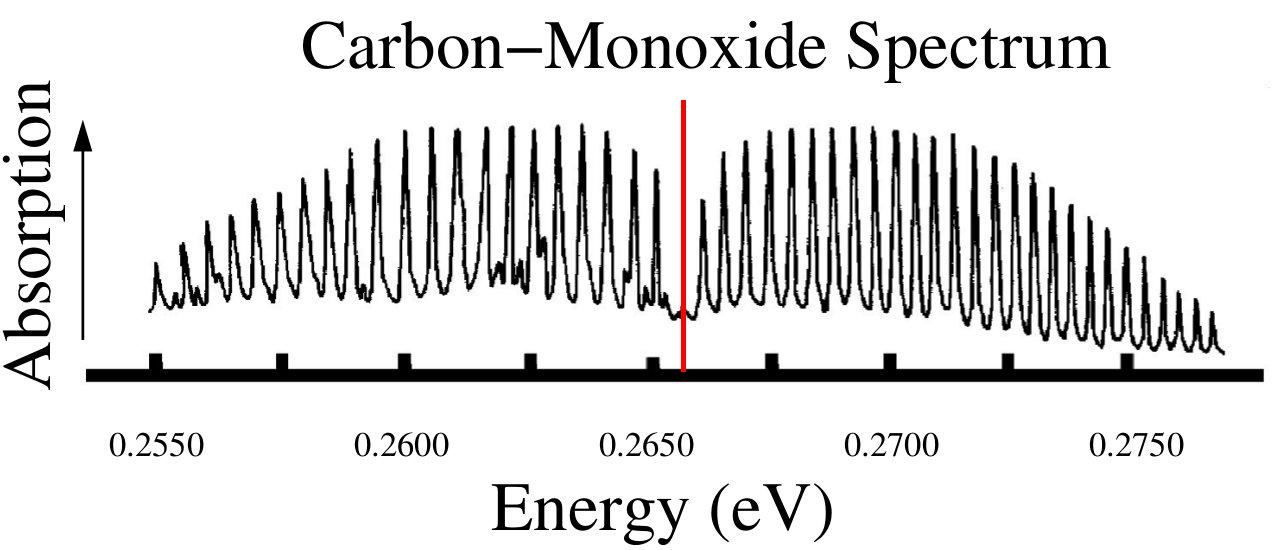
- Recall again the vibration-rotation spectrum of carbon monoxide shown in the figure above.
How would it change (if at all) if you replaced the oxygen (
 ) and carbon (
) and carbon ( ) atoms with sulfur (
) atoms with sulfur ( ) and magnesium
(
) and magnesium
( ) atoms each with twice the mass of the oxygen and carbon respectively.
Assume the separation of the new atoms is the same as in the
) atoms each with twice the mass of the oxygen and carbon respectively.
Assume the separation of the new atoms is the same as in the 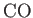 molecule.
Explain your reasoning.
molecule.
Explain your reasoning.
- A harmonic oscillator is in the state
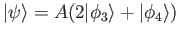 What is
What is 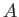 ? Show your reasoning.
? Show your reasoning.
- The claim is made that the free particle eigenfunction
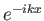 corresponds to a wave traveling
to the right. Is that true? Explain your reasoning.
corresponds to a wave traveling
to the right. Is that true? Explain your reasoning.
- Why do we express the wave function in terms of energy eigenstates?
- For an electron in the three-dimensional hydrogen atom is the following uncertainty relationship
correct?
The
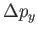 part refers to the uncertainty in the
part refers to the uncertainty in the  component of the electron. Explain your reasoning.
component of the electron. Explain your reasoning.
- For the step barrier shown in the figure, what is the solution to the Schrödinger
equation in each region and what are the boundary conditions those solutions must satisfy.
Express your answer in terms of the mass
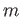 , energy
, energy 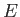 , potential
, potential 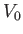 , and any other constants.
, and any other constants.
Do not write below this line.
- For a particle in a box in the
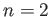 state as shown in the figure, the probability
density at certain points is zero.
Does this imply the particle cannot move across those points? Explain.
state as shown in the figure, the probability
density at certain points is zero.
Does this imply the particle cannot move across those points? Explain.
- Consider the potential barrier shown below.
How would you use the transfer-matrix approach to connect the wave function
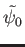 in region 0
to the wave function
in region 0
to the wave function
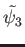 in region 3?
Give your answer in the appropriate notation used in class for the discontinuity and
propagation matrices.
What is the form of the wave number
in region 3?
Give your answer in the appropriate notation used in class for the discontinuity and
propagation matrices.
What is the form of the wave number 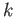 in each region?
in each region?
Problems. Clearly show all work for full credit on a separate piece of paper.
Do not write below this line. Continue to the next page.
| 2. (10 pts.) |
A thousand quarks are trapped in a one-dimensional box in the
range 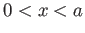 .
At
.
At  each particle is in the state
each particle is in the state
where
The eigenfunctions and eigenvalues for this particle in a box
are
and
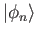 is zero outside the box.
How many particles are in the interval
is zero outside the box.
How many particles are in the interval 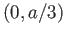 at
at  ?
Get your answer in terms of
?
Get your answer in terms of 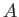 ,
, 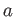 , and any other constants.
, and any other constants.
|
| 3. (10 pts.) |
In studying rotational motion, we take advantage of the
center-of-mass system to make life easier.
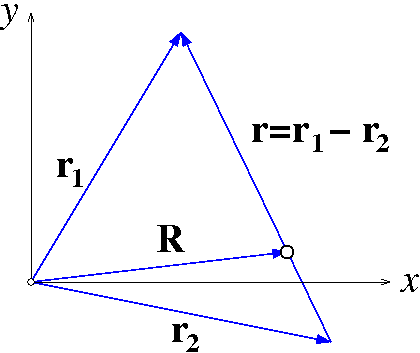
Consider the two-particle system shown in the figure including the
center-of-mass vector  .
For convenience we will place our origin at the center-of-mass of
the system (
.
For convenience we will place our origin at the center-of-mass of
the system (
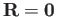 ).
Show the classical mechanical energy of the two-particle system in the center-of-mass frame
can be written as
).
Show the classical mechanical energy of the two-particle system in the center-of-mass frame
can be written as
and 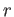 is the relative coordinate between the two
particles as shown in the figure. Notice that
is the relative coordinate between the two
particles as shown in the figure. Notice that 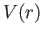 depends only on
the relative coordinate.
depends only on
the relative coordinate.
|
| 4. (10 pts.) |
Consider a time-independent Schrödinger equation,
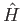 , that is composed of two independent
parts, so that
, that is composed of two independent
parts, so that
The two parts of the Hamiltonian have solutions
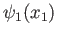 and
and
 such that
such that
Show the wave function of the composite system  is the following.
is the following.
|
| 5. (15 pts.) |
Another thousand quarks are trapped in a same-sized-as-above, one-dimensional box.
This time at  each particle is in the following (different than before) state
each particle is in the following (different than before) state
where
 .
The eigenfunctions and eigenvalues for this particle in a box
are the same as in Problem 2.
How many particles have energy
.
The eigenfunctions and eigenvalues for this particle in a box
are the same as in Problem 2.
How many particles have energy 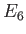 at
at  ? You should get a number for this.
? You should get a number for this.
|
| 6. (15 pts.) |
A pion is in a harmonic potential (i.e., it feels
a Hooke's-Law-like force) and has the initial wave
function
where 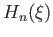 are the Hermite polynomials and
are the Hermite polynomials and
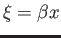 where
where
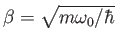 .
The eigenfunctions and eigenvalues of the particle are
.
The eigenfunctions and eigenvalues of the particle are
- What is the average value of the energy for this state in terms
of
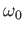 and any other constants?
and any other constants?
- What are the probabilities of finding the pion in
the
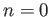 ,
, 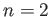 , and
, and 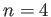 states?
states?
- What is
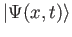 for
for 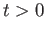 ?
Express your answer in terms of
?
Express your answer in terms of 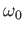 and any other necessary
constants.
and any other necessary
constants.
|
Do not write below this line.
Physics 309 Equations
The wave function,
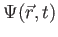 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 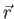 to
to
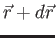 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
 and
and
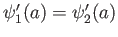 ) .
) .
Constants
Speed of light (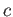 )
) |

|
fermi (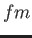 )
) |

|
Boltzmann constant (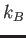 )
) |
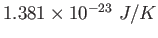
|
angstrom (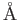 )
) |
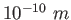
|
|
|
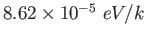
|
electron-volt (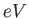 )
) |
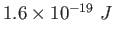
|
Planck constant (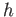 )
) |
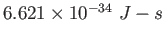
|
MeV |
|
|
|
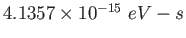
|
GeV |
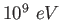
|
Planck constant (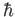 )
) |
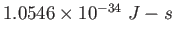
|
Electron charge (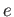 )
) |
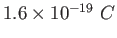
|
|
|
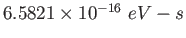
|
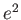
|

|
Planck constant (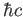 )
) |
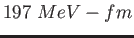
|
Electron mass (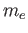 )
) |
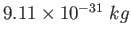
|
|
|
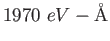
|
|

|
Proton mass ( )
) |
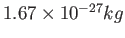
|
atomic mass unit (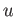 )
) |
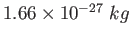
|
|
|

|
|
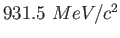
|
Neutron mass (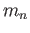 )
) |
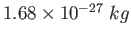
|
|
|
|
|
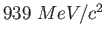
|
|
|
Integrals and Derivatives
Hermite polynomials (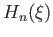 )
)

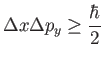

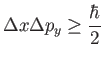
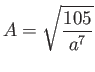
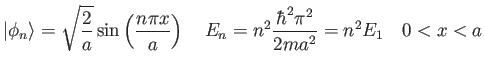
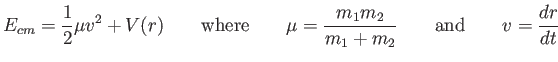
![$\displaystyle \vert\Psi(x,0)\rangle =
e^{-\xi^2/2} \left [\frac{ H_0(\xi) - \sqrt 2 H_2(\xi) - H_3(\xi) + H_5(\xi) + H_6(\xi)}{\sqrt 6} \right ]
$](img59.png)


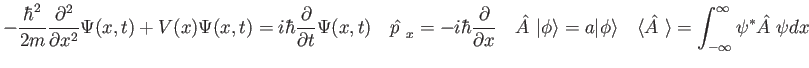

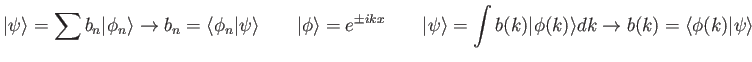

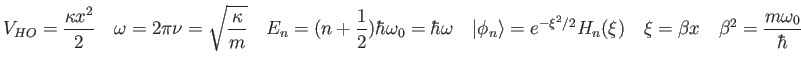
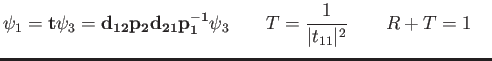



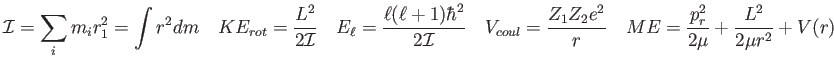
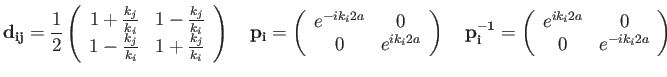
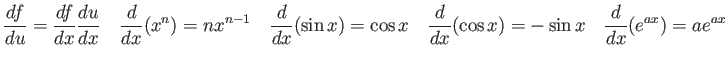
![$\displaystyle \frac{d}{dx}(\ln ax) = \frac{1}{x} \quad
\int x^n dx = \frac{x^{n...
...frac{1}{\sqrt{x^2 + a^2}} dx = \ln \left [ x + \sqrt{x^2 + a^2} \right ] \quad
$](img124.png)
![$\displaystyle \int \frac{x}{\sqrt{x^2 + a^2}} dx = \sqrt{x^2 + a^2} \quad
\int ...
...t{x^2 + a^2} - \frac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \quad
$](img125.png)
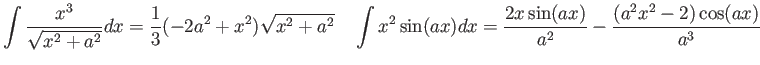

![]() )
)