| A. |
|
| B. |
|
| C. |
|
| D. |
|
| E. |
|
![\includegraphics[height=1.250in]{fermi.eps}](img109.png)
| A. |
|
D. |
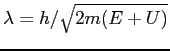 |
| B. |
|
E. |
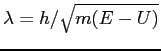 |
| C. |
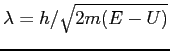 |
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (3 pts. apiece) Answer questions 1-6 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 7-8 circle the correct answer.
| A. |
|
| B. |
|
| C. |
|
| D. |
|
| E. |
|
![\includegraphics[height=1.250in]{fermi.eps}](img109.png)
| A. |
|
D. |
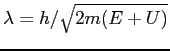 |
| B. |
|
E. |
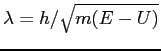 |
| C. |
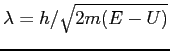 |
Problems. Clearly show all work for full credit.
| 1. (12 pts.) |
A beam of |
Problems (continued). Clearly show all work for full credit.
| 2. (12 pts) |
An electron moves in a three-dimensional cube of side
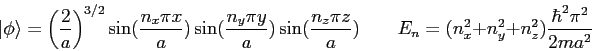
where 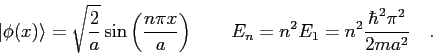
|
| 3. (12 pts) |
A harmonic oscillator consists of a mass |
| 4. (12 pts) |
If |
| 5. (14 pts) |
At
|
| 6. (14 pts) |
A particle moving in one dimension has the wave function
where
|
Equations
The wave function,
![]() , contains all we know of a system and
its
square is the probability of finding the system in the region
, contains all we know of a system and
its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2)
continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2)
continuous, and (3) single-valued.
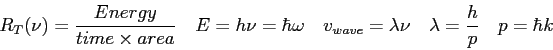
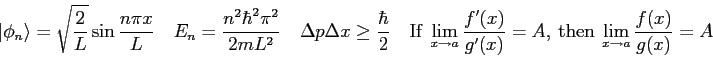
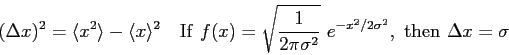
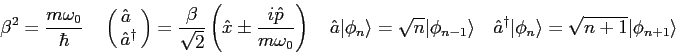
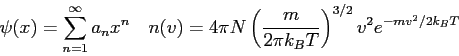

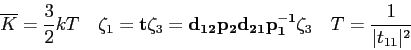
![\begin{displaymath}
R+T = 1 \quad
T_{WKB} = \exp\left [ -2 \int_{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img65.png)
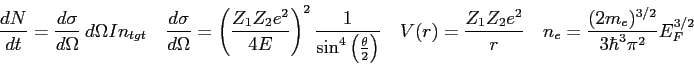
Conversions and Constants
| Speed of light ( |
|
fermi ( |
|
| Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
| Planck constant ( |
|
MeV | |
|
|
GeV | ||
| Planck constant ( |
|
Electron charge ( |
|
|
|
|||
| Planck constant ( |
Electron mass ( |
|
|
|
|
|||
| Proton mass ( |
|
atomic mass unit ( |
|
| Neutron mass ( |
|
Avogadro's Number |
|
| ( |
![\includegraphics[width=6.5in]{periodic_chart2.eps}](img108.png)