| 3. |
25 pts. |
In the phenomenon of cold emission, electrons are drawn from a metal
(at room temperature) by an externally supported electric field.
The potential well that the metal presents to the free electrons before
the electric field is turned on is depicted in the left-hand side
of the
figure below.
After application of the constant electric field 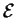 ,
the potential at the surface slopes down as shown in the right-hand side
of the figure below, thereby allowing electrons from the Fermi
sea to ``tunnel'' through the potential barrier.
If the surface of the metal is taken as the ,
the potential at the surface slopes down as shown in the right-hand side
of the figure below, thereby allowing electrons from the Fermi
sea to ``tunnel'' through the potential barrier.
If the surface of the metal is taken as the 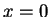 plane, the new potential
outside the surface is plane, the new potential
outside the surface is
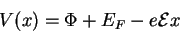
where 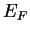 is the Fermi level and is the Fermi level and 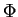 is the work function of
the metal. is the work function of
the metal.
- Use the WKB approximation to calculate the transmission
coefficient for cold emission.
- Estimate the field strength
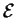 , in , in 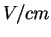 (or (or
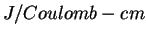 ), necessary to
draw a current density of ), necessary to
draw a current density of 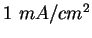 from a potassium surface.
You need to use the expression from a potassium surface.
You need to use the expression
where 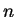 is the electron density and is the electron density and 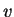 is the speed of the
electrons at the top of the Fermi sea.
The expression for is the speed of the
electrons at the top of the Fermi sea.
The expression for 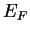 is is
and has a value 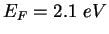 for potassium.
The work function for potassium.
The work function 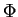 for potassium is also for potassium is also 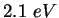 . .
![\includegraphics[]{emission.eps}](img25.png)
|
![]() and
and ![]() .
The eigenfunctions and eigenvalues are
.
The eigenfunctions and eigenvalues are
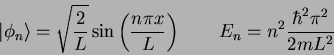
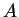 ?
?
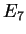 at
at  ?
You should get a final, numerical answer.
?
You should get a final, numerical answer.
![]() , at what value of
, at what value of ![]() is the probability density in Region 2
one-quarter the density of particles in the incident beam?
You're answer should be in terms of the constants of the
problem (i.e.,
is the probability density in Region 2
one-quarter the density of particles in the incident beam?
You're answer should be in terms of the constants of the
problem (i.e., ![]() , the wave numbers, etc.).
, the wave numbers, etc.).
![\includegraphics[]{step.eps}](img11.png)
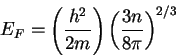
![\includegraphics[]{emission.eps}](img25.png)