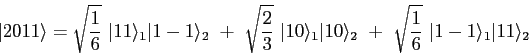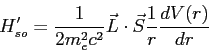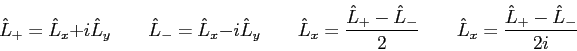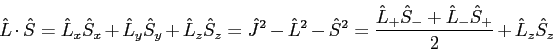Physics 402 Test 2
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Multiple Choice Questions (Circle your choice, 4 points apiece).
- The Stern-Gerlach experiment in quantum physics demonstrates the
quantization of spin.
Sample data are shown in the figure.
The conclusion is that
| (a) |
the electron is a fermion and can have spin up or down |
(d) |
The electron can only have spin down |
| (b) |
the electron has no spin |
(e) |
the electron is a fermion and can have spin 3/2, 1/2, -1/2, -3/2 |
| (c) |
the electron can only have spin up |
|
|
![\includegraphics[height=1.5in]{f1.eps}](img92.png)
- Consider a mechanical model of the proton where the spin is due to
its rotation.
Assume the proton to be a uniform, solid sphere and derive the
equatorial velocity.
Assume
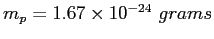 and
and
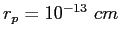 .
.
- In the Zeeman effect, the energy of a spectral line is found to be
changed in a magnetic field.
What is the amount of the energy change?
- A plane wave solution of the electromagnetic wave equation is
Under what conditions is this light circularly polarized?
| (a) |
 |
(d) |
 and and
 |
| (b) |
 and and
 |
(e) |
 and and
 |
| (c) |
 and and
 |
|
|
Problems. Clearly show all work for full credit.
| 2. (32 pts.) |
Using the expressions for
 and and  shown below operate
with shown below operate
with  on the
following uncoupled angular
momentum state for two on the
following uncoupled angular
momentum state for two  electrons electrons
to verify the  entry for the entry for the
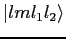 eigenstate. eigenstate.
|
| 3. (32 pts.) |
We used the Coulomb potential to describe the
interaction between the proton and electron in our initial,
simple model of the hydrogen atom.
We used perturbation theory to incorporate the
spin-orbit interaction into the model using
where 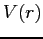 is the potential energy between the electron and
the proton.
Suppose now the proton and electron are part of some larger
molecule and we can now more accurately describe the
interaction using a harmonic oscillator potential.
Recall that the harmonic oscillator potential energy
is is the potential energy between the electron and
the proton.
Suppose now the proton and electron are part of some larger
molecule and we can now more accurately describe the
interaction using a harmonic oscillator potential.
Recall that the harmonic oscillator potential energy
is 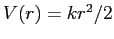 and the energy levels of an unperturbed
oscillator are and the energy levels of an unperturbed
oscillator are
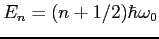 .
What is the effect of the spin-orbit interaction on the
spectrum of harmonic oscillator states?
In other words, what energy shifts does this perturbation
cause? .
What is the effect of the spin-orbit interaction on the
spectrum of harmonic oscillator states?
In other words, what energy shifts does this perturbation
cause?
You might find some of the following expressions useful.
|
Table of Constants
| Speed of light |
 |
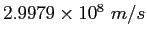 |
| Boltzmann's constant |
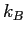 |
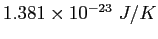 |
| |
|
 |
| Planck's constant |
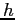 |
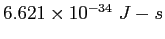 |
| |
|
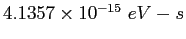 |
| |
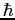 |
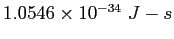 |
| |
|
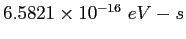 |
| |
 |
 |
| |
 |
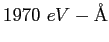 |
| Electron charge |
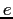 |
 |
| Electron mass |
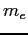 |
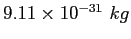 |
| |
|
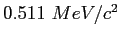 |
| Proton mass |
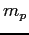 |
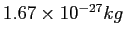 |
| |
|
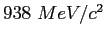 |
| Neutron mass |
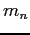 |
 |
| |
|
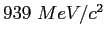 |
| atomic mass unit |
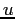 |
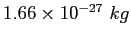 |
| |
|
 |
| Fine structure constant |
 |
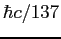 |
Rotational Inertias
| Hoop about central axis |
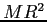 |
| Annular ring about central axis |
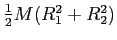 |
| Solid disk about central axis |
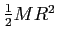 |
| Solid disk about central diameter |
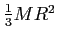 |
| Solid sphere about any diameter |
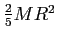 |
| Thin spherical shell about any
diameter |
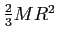 |
Trigonometric Identities
![\includegraphics[height=1.5in]{f1.eps}](img92.png)