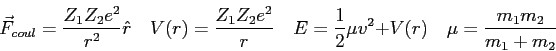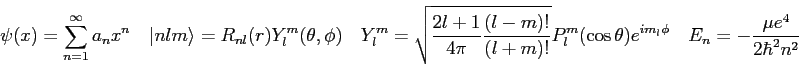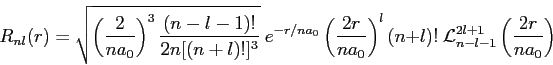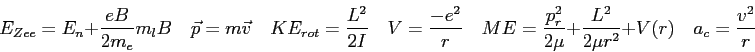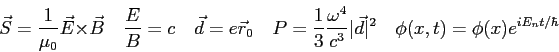
I pledge that I have given nor received unauthorized assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (6 pts. apiece) Answer questions in complete, well-written sentences WITHIN the spaces provided.

Problems. Answer the questions below on a separate sheet of paper. Clearly show all work for full credit.
| 1. (10 pts.) |
In the Bohr model of the hydrogen atom, the electron
is in a circular orbit at a radius of
|
||||||||||||||||||
| 2. (10 pts.) |
In a region of free space, the electric field of an electromagnetic wave is
|
||||||||||||||||||
| 3. (20 pts.) |
In our theory of radiation emission from hydrogen the matrix element of
the
Using this result and the equations listed below, generate selection rules. Clearly show your reasoning and identify any equations you use from the list below.
|
More Problems. Answer the questions below on a separate sheet of paper. Clearly show all work for full credit.
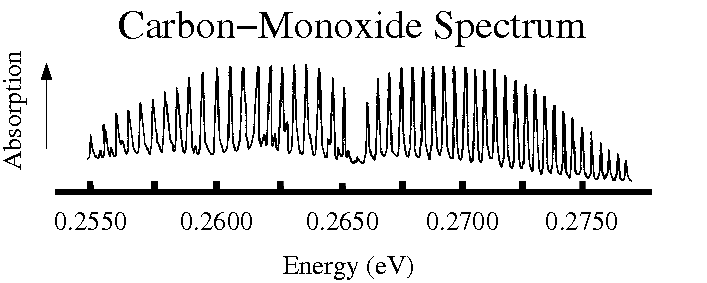
| 4. (30 pts) |
A 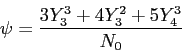
|
|
Speed of light ( |
|
fermi ( |
|
|
Boltzmann constant ( |
|
angstrom ( |
|
|
|
electron-volt ( |
|
|
|
Planck constant ( |
|
MeV | |
|
|
GeV | |
|
|
Planck constant ( |
|
Electron charge ( |
|
|
|
|
|
|
|
Planck constant ( |
|
Electron mass ( |
|
|
|
|
||
|
Proton mass ( |
|
atomic mass unit ( |
|
| |
|
||
|
Neutron mass ( |
|
Avogadro's Number ( |
|
| |
|||
|
Permeability of free space ( |
|
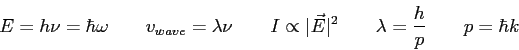
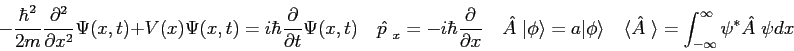
cmrThe wave function,
![]() , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
![]() and
and
![]() ) .
) .