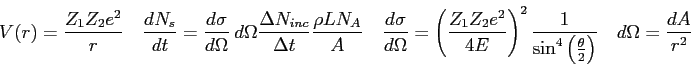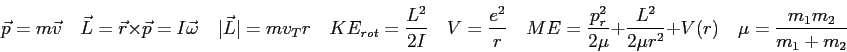Physics 310 Test 1
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (6 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided.
- Recall your comparison of theory and data in the alpha decay lab. What did the theory get right? What is at least one weakness in the theory?
- What is the quantum program?
- List a measurement we discussed in class that requires quantum mechanics to explain it and describe how classical physics failed in that explanation.
- When we solved the rectangular barrier problem we required the wave function to continuous across the boundary between
different potential energy regions. Why?
- In solving the carbon-monoxide problem we choose the origin of our coordinate system to be on the center-of-mass of the molecule.
Why?
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
Recall your calculation of the total derivative 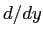 for homework. Show for homework. Show
(Hint: Use the fact that
 where where
 and and
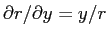 .) .)
The transformation from Cartesian coordinates to spherical
coordinates is
|
| 2. (20 pts.) |
A beam of 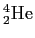 ( (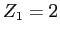 , , 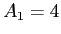 ), i.e. ), i.e. 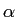 -particles,
of kinetic energy -particles,
of kinetic energy 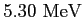 and intensity
and intensity
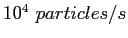 , is incident on a gold foil
( , is incident on a gold foil
(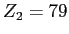 , , 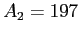 ) of density ) of density 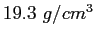 and thickness and thickness
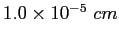 .
A detector of area .
A detector of area 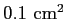 is placed at a distance of is placed at a distance of  from the
foil. If from the
foil. If  is the angle between the incident beam and a line from the
center of the foil to the center of the detector and the differential cross section for
Rutherford scattering at is the angle between the incident beam and a line from the
center of the foil to the center of the detector and the differential cross section for
Rutherford scattering at
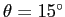 is is
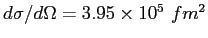 , then what is
the count rate? , then what is
the count rate?
|
| 3. (30 pts) |
A particle in incident on a step barrier of height  as shown in the figure.
The components of the wave function in different regions are also shown in the figure.
What is the reflection coefficient in terms of the wave numbers as shown in the figure.
The components of the wave function in different regions are also shown in the figure.
What is the reflection coefficient in terms of the wave numbers 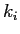 ?
Leave your answer in symbolic form. ?
Leave your answer in symbolic form.
|
Physics 310 Equations and Constants
The wave function,
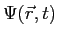 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 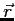 to
to
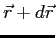 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
Speed of light ( ) ) |
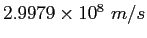 |
fermi (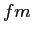 ) ) |
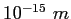 |
Boltzmann constant (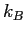 ) ) |
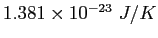 |
angstrom (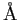 ) ) |
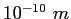 |
|
|
 |
electron-volt (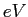 ) ) |
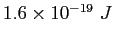 |
Planck constant (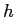 ) ) |
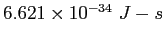 |
MeV |
 |
|
|
 |
GeV |
 |
Planck constant ( ) ) |
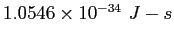 |
Electron charge ( ) ) |
 |
|
|
 |
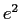 |
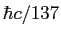 |
Planck constant (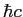 ) ) |
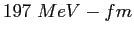 |
Electron mass ( ) ) |
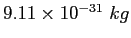 |
|
|
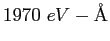 |
|
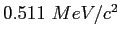 |
Proton mass (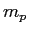 ) ) |
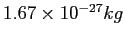 |
atomic mass unit (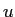 ) ) |
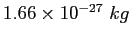 |
|
|
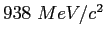 |
|
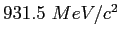 |
Neutron mass (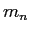 ) ) |
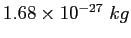 |
Avogadro's Number ( ) ) |
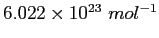 |
|
|
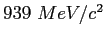 |
|
|
![]() for homework. Show
for homework. Show
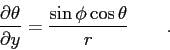
![]() where
where
![]() and
and
![]() .)
.)
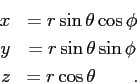
![]() (
(![]() ,
, ![]() ), i.e.
), i.e. ![]() -particles,
of kinetic energy
-particles,
of kinetic energy ![]() and intensity
and intensity
![]() , is incident on a gold foil
(
, is incident on a gold foil
(![]() ,
, ![]() ) of density
) of density ![]() and thickness
and thickness
![]() .
A detector of area
.
A detector of area ![]() is placed at a distance of
is placed at a distance of ![]() from the
foil. If
from the
foil. If ![]() is the angle between the incident beam and a line from the
center of the foil to the center of the detector and the differential cross section for
Rutherford scattering at
is the angle between the incident beam and a line from the
center of the foil to the center of the detector and the differential cross section for
Rutherford scattering at
![]() is
is
![]() , then what is
the count rate?
, then what is
the count rate?
![]() as shown in the figure.
The components of the wave function in different regions are also shown in the figure.
What is the reflection coefficient in terms of the wave numbers
as shown in the figure.
The components of the wave function in different regions are also shown in the figure.
What is the reflection coefficient in terms of the wave numbers ![]() ?
Leave your answer in symbolic form.
?
Leave your answer in symbolic form.
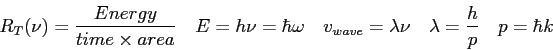
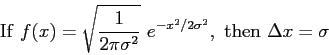
![\begin{displaymath}
\psi_1 =
{\bf t} \psi_3 =
{\bf d_{12} p_2 d_{21} p_1^{-1...
..._{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img34.png)