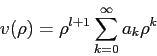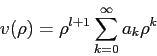Physics 310
Solving the Radial Part of the Hydrogen Atom Wave Function
- The three-dimensional Schroedinger equation can be written in
spherical coordinates as
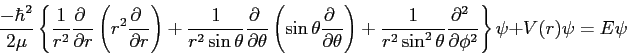 |
(1) |
where 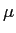 is the reduced mass.
Assuming the solution is separable so
is the reduced mass.
Assuming the solution is separable so
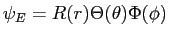 and using the eigenvalues of the hydrogen atom
show that Equation 1 can rewritten as
and using the eigenvalues of the hydrogen atom
show that Equation 1 can rewritten as
![\begin{displaymath}
\frac{\partial}{\partial r} \left ( r^2 \frac{\partial R}{\p...
...
\left[ E - V - \frac{\hbar^2}{2\mu r^2}l (l+1) \right ] R = 0
\end{displaymath}](img4.png) |
(2) |
- Let
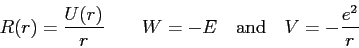 |
(3) |
and show Equation 2 can be rewritten as
![\begin{displaymath}
-\frac{\partial^2 U}{\partial r^2} +
\left [ \frac{l(l+1)}...
...{\hbar^2}\frac{e^2}{r} + \frac{2\mu W}{\hbar^2} \right ] U = 0
\end{displaymath}](img6.png) |
(4) |
- Now let
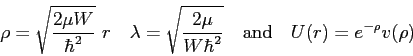 |
(5) |
and rewrite Equation 4 as
![\begin{displaymath}
\frac{\partial^2 v}{\partial \rho^2} - 2\frac{\partial v}{\p...
...frac{\lambda e^2}{\rho} - \frac{l(l+1)}{\rho^2} \right ] v = 0
\end{displaymath}](img8.png) |
(6) |
- Here we apply the method of Frobenius to generate a solution to Equation 6.
Assume the following form for
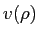 .
.
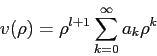 |
(7) |
and generate the recurrence relationship
} a_k
\end{displaymath}](img11.png) |
(8) |