Physics 309
Magnetic Interactions in the Hydrogen Atom
- In the Bohr model of the hydrogen atom (i.e. much
like the classical mini-solar system picture), the electron
is in a circular orbit at a radius of
 .
What is the current produced by the electron in terms of
its speed
.
What is the current produced by the electron in terms of
its speed 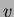 , its charge
, its charge 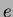 , and the radius of its
orbit
, and the radius of its
orbit 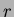 ?
Show that
?
Show that
where 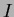 is the current produced by the electron.
is the current produced by the electron.
- For the electron in the Bohr atom use
the Biot-Savart Law to show that
the magnetic field produced at the center of the orbit
(i.e., at the location of the proton) is
where 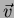 is the electron velocity and
is the electron velocity and 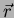 is the
electron position vector.
The expression above uses MKS units.
is the
electron position vector.
The expression above uses MKS units.
- What is the electric field produced by the electron at
the position of the proton?
Use this expression to show that
where 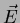 is the electron's electric field.
The expression above uses MKS units.
is the electron's electric field.
The expression above uses MKS units.
- Use the above results to show
that the magnetic field produced by the electron
at the position of the proton is