
What is the transfer matrix for the rectangular barrier in terms of the appropriate wave numbers? What is the transmission coefficient? Is your expression consistent with the one in your text? Why or why not?
- Calculate the inter-nuclear distance
when the proton and the
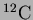 are just touching
and call this distance
are just touching
and call this distance 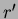 .
Estimate the Coulomb barrier,
.
Estimate the Coulomb barrier, 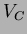 , between the proton and the
carbon nucleus.
, between the proton and the
carbon nucleus.
- The proton is incident on the carbon nucleus because of its
thermal motion in the
Sun's core.
Estimate the incident energy of the proton by assuming
that its energy is
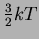 where
where  is Boltzman's constant
(
is Boltzman's constant
(
 ) and
) and
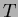 is the temperature of the solar core (
is the temperature of the solar core (
 ).
).
- Fusion will occur when the proton can tunnel through
the barrier.
Treat the Coulomb barrier as a rectangular barrier
and calculate the transmission coefficient.
Justify your choice for the width and the height of the barrier.
Do you expect solar fusion to be a speedy process?
Cite any other evidence that would support your result.