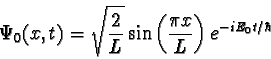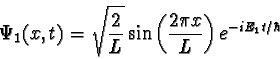Physics 309 Homework
A Particle in a Box
Consider a particle of mass mthat is freely allowed to move along the x axis in the
region
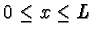 ,
but
is strictly forbidden to be outside
this region.
The particle bounces between the impenetrable
walls located at x=0 and x=L.
The wave functions for the ground and first excited
states are
,
but
is strictly forbidden to be outside
this region.
The particle bounces between the impenetrable
walls located at x=0 and x=L.
The wave functions for the ground and first excited
states are
and
for the region within the walls and are zero outside.
- 1.
- Draw a schematic picture of the potential energy.
- 2.
- Determine an expression for the energy in each case in
terms of the other constants in the problem.
- 3.
- Plot the spatial dependence
of the wave functions for each state using Mathematica.
Purely on the
basis of these plots how could one identify which state is the
high energy one?
- 4.
- Calculate the expectation value of the position xfor each state of the system.
Is your result consistent with the plots in part 3. Why?
![]() ,
but
is strictly forbidden to be outside
this region.
The particle bounces between the impenetrable
walls located at x=0 and x=L.
The wave functions for the ground and first excited
states are
,
but
is strictly forbidden to be outside
this region.
The particle bounces between the impenetrable
walls located at x=0 and x=L.
The wave functions for the ground and first excited
states are