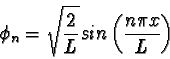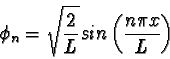Physics 309 Homework
Orthonormality
The wave functions that are solutions to the Schroedinger
equation for a particle in an infinite square well potential are
where the walls of the `box' lie at x=0 and
x=L.
- 1.
- What are the energy eigenvalues and eigenfunctions of a particle
in an infinite square well potential in terms of the mass of the particle,
the size of the box, and any other physical constants?
- 2.
- Show analytically that they comprise an
orthonormal set of functions.
It may be worthwhile to use the integrating power of
Mathematica here.
To obtain an indefinite integral of say sin2 x use the following
command:
``Integrate[ Sin[x]^ 2, x] ''.
To find a definite integral for the same function over the range 0-2
use the following syntax:
``Integrate[ Sin[x]^ 2,
 x, 0, 2
x, 0, 2  ] ''.
] ''.
- 3.
- Once you have completed the analytical part
of your argument use Mathematica to demonstrate visually
the properties of
the eigenfunctions
that lead to this orthonormality.
(Hint: What features of the integrand of the inner product between states
with different values of the quantum number n imply the inner product
is zero?)