Physics 401
Numerical Solutions to
Second Order Differential Equations
- Show the second-order correction to the
Taylor-series formula for the second derivative of a function f(x)
is
where 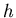 is the stepsize.
is the stepsize.
- Use a Taylor-series method to generate an algorithm for estimating
the
first derivative of a function.
What is the size of the error?
- Generate a recursion relation equation for the following
equations using the Taylor-series formula for the second derivative.
State the order of the error for each result.
- Hooke's Law states the force exerted by a spring
is proportional to its displacement from its equilibrium
position or
where 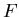 is the force exerted by the spring,
is the force exerted by the spring, 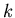 is the spring constant,
and
is the spring constant,
and 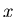 is the displacement from the equilibrium point (see the discussion
on harmonic motion in Halliday, Resnick, and Walker).
is the displacement from the equilibrium point (see the discussion
on harmonic motion in Halliday, Resnick, and Walker).
- Write Hooke's Law as linear, second-order differential
equation.
- What is the general solution of the equation in the previous part?
Find the particular solution for the initial conditions:
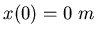 ,
,
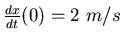 .
Assume k/m = 1.0 kg/
.
Assume k/m = 1.0 kg/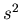 .
.
- Use a Taylor-series method to generate an algorithm
for solving the differential equation.
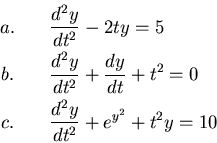
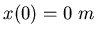 ,
,
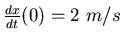 .
Assume k/m = 1.0 kg/
.
Assume k/m = 1.0 kg/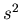 .
.