Physics 309
Commutators and Hermitian Operators
- What is the commutator of the momentum
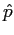 and energy
and energy 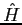 operators?
Can you draw any conclusions about the eigenfunctions of
operators?
Can you draw any conclusions about the eigenfunctions of 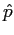 and
and 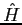 ?
?
- If the operator
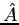 is hermitian show
is hermitian show
- Show that for two hermitian operators,
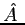 and
and 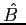 , if
, if
then
as well, where
- For the definition of the inner product in one dimension that we have been using in class,
show
where
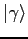 is an element/eigenfunction of a Hilbert space.
is an element/eigenfunction of a Hilbert space.
- Show that for any two elements
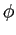 and
and 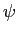 in a Hilbert space
with lengths/norms
in a Hilbert space
with lengths/norms 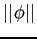 and
and 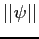 the Cauchy-Schwart Inequality is true
the Cauchy-Schwart Inequality is true
where
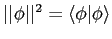 .
This is the same problem as 4.20 in Liboff, but with the hint below added.
.
This is the same problem as 4.20 in Liboff, but with the hint below added.
Hint: Let
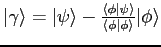 and use the result in the previous problem.
and use the result in the previous problem.
![]() and use the result in the previous problem.
and use the result in the previous problem.
![]() and use the result in the previous problem.
and use the result in the previous problem.