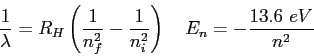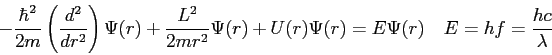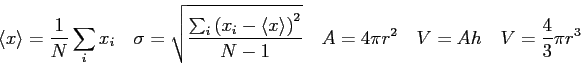Physics 132-04 Test 3
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 for 8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- During the radioactivity laboratory you made several runs with the radiation counter with no radioactive
sources nearby. Why?
- Radiocarbon dating relies on the observation that the fraction of
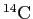 in living organisms has
been at least roughly constant for many thousands of years.
How can this be if the
in living organisms has
been at least roughly constant for many thousands of years.
How can this be if the 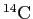 is constantly decaying away?
is constantly decaying away?
- In building the theory behind the two-slit interference pattern we derived an expression for the intensity
of pure, 2-slit interference (no diffraction effects). The result is shown in the top figure below.
The measured result for the intensity looks more like the bottom figure.
Why are the two so different?
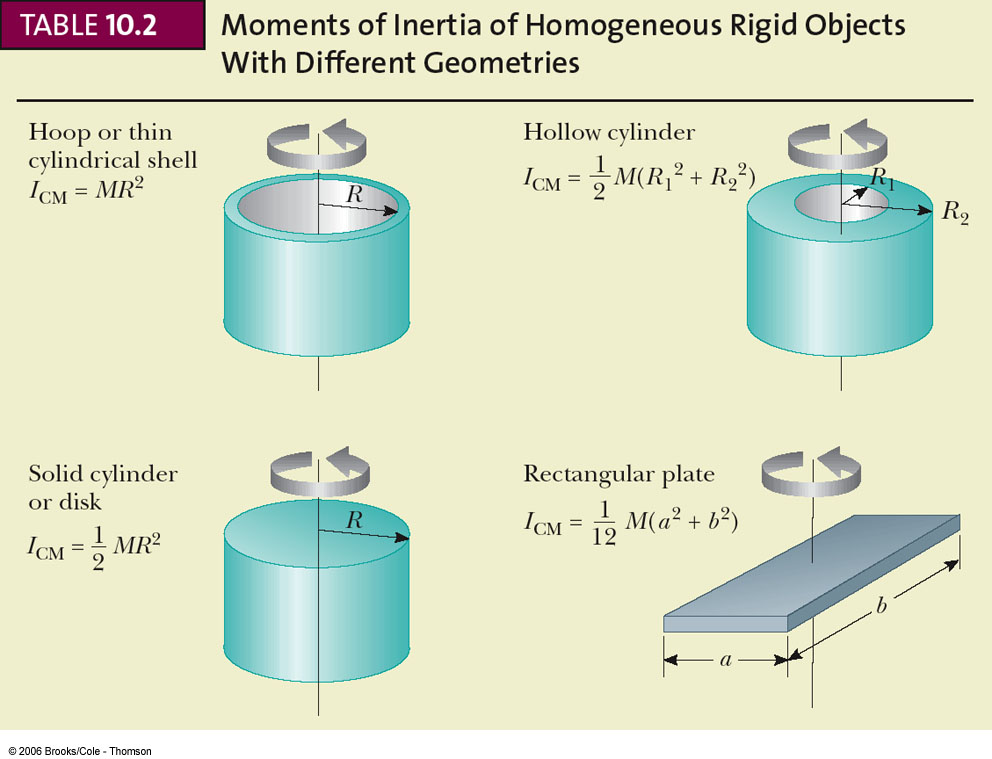
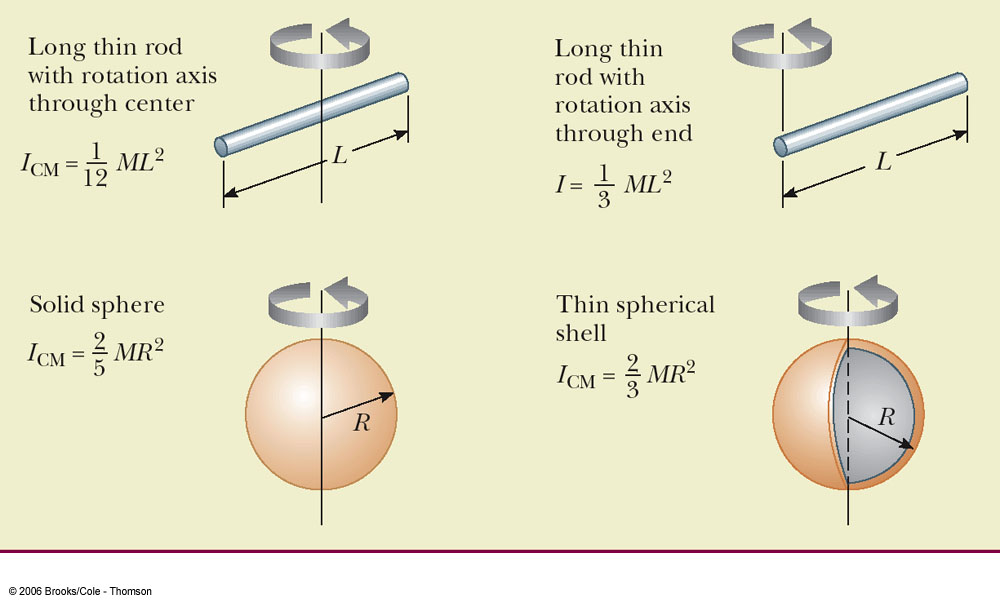
- Recall the laboratory on conservation of angular momentum where you analyzed
a rotational collision where a cylindrical weight of mass
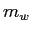 and radius
and radius 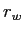 was dropped on a rotating disk and ended up revolving about the origin at a distance
was dropped on a rotating disk and ended up revolving about the origin at a distance
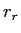 .
The distance
.
The distance 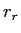 is from the center of the rotator to the
center of the dropped weight.
Generate an expression for the moment of inertia of the dropped weight
in terms of the quantities listed here.
is from the center of the rotator to the
center of the dropped weight.
Generate an expression for the moment of inertia of the dropped weight
in terms of the quantities listed here.
- Induction furnaces are commonly used in industry to take advantage of
electromagnetic induction to heat metals.
How would such a device work and what things would you need to build one?
Problems (3). Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
DO NOT WRITE BELOW THIS LINE.
| 2. |
18 pts. |
The radionuclide 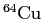 has a half-life of has a half-life of
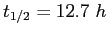 .
How many nuclei from an initially pure, 10-g sample of .
How many nuclei from an initially pure, 10-g sample of 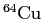 will
decay during the 3.0-hour period beginning 10.0 hours later? will
decay during the 3.0-hour period beginning 10.0 hours later?
|
| 3. |
24 pts. |
Laser light with a wavelength
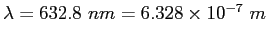 is directed through one slits or two slits and falls on a screen a distance
is directed through one slits or two slits and falls on a screen a distance
 away.
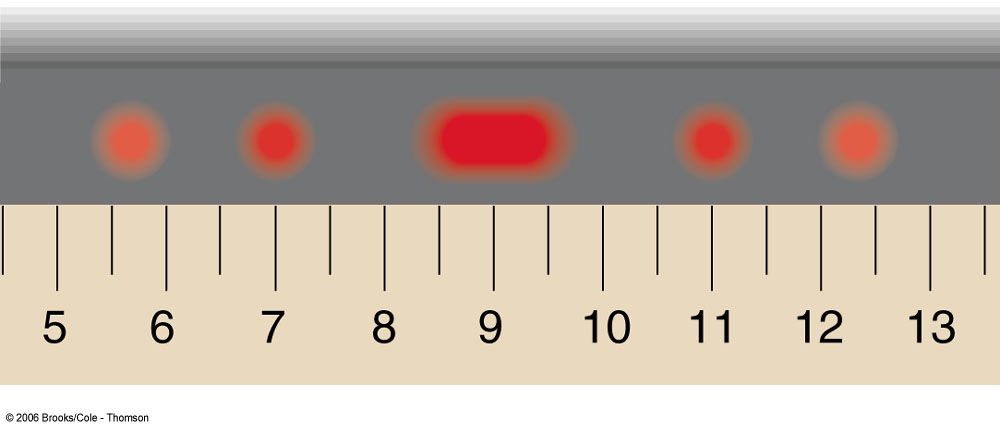
The figure below shows the pattern on the screen with a centimeter ruler below it.
Did the light pass through one slit or two slits?
Explain your reasoning.
It the light passed through one slit find its width.
If the light passed through two slits find the distance between their centers. away.
The figure below shows the pattern on the screen with a centimeter ruler below it.
Did the light pass through one slit or two slits?
Explain your reasoning.
It the light passed through one slit find its width.
If the light passed through two slits find the distance between their centers.
|
Physics 132-4 Constants
Avogadro's number (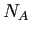 ) ) |
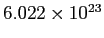 |
Speed of light (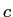 ) ) |
 |
 |
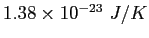 |
proton/neutron mass |
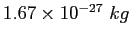 |
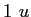 |
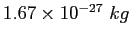 |
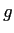 |
 |
| Gravitation constant |
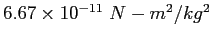 |
Earth's radius |
 |
Coulomb constant (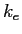 ) ) |
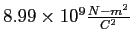 |
Electron mass |
 |
Elementary charge ( ) ) |
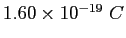 |
Proton/Neutron mass |
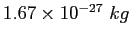 |
Permittivity constant (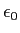 ) ) |
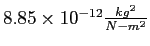 |
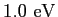 |
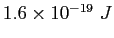 |
 |
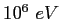 |
atomic mass unit ( ) ) |
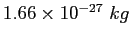 |
Physics 132-4 Equations
The Periodic Chart.
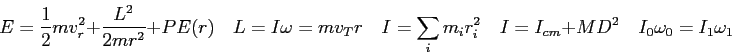
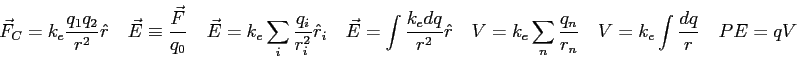
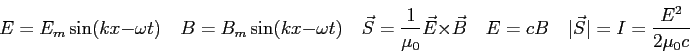
![\begin{displaymath}
I = 4 I_0 \cos^2 \left ( {\pi d \over \lambda} \sin \theta \...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img49.png)