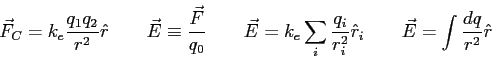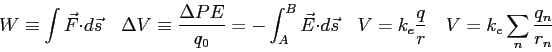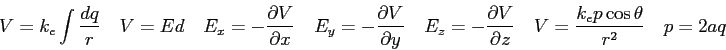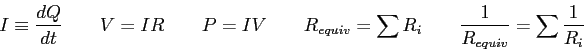Physics 132-04 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 for 8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Draw what you think the field lines and equipotential lines between parallel plates
will look like. Explain you reasoning.
- In our simulations of the electric potentials for a point charge and for an electric dipole
we found they behaved differently as a function of the distance
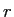 from origin.
Did the electric dipole potential fall faster, slower, or the same as the point charge?
Explain the result you observed.
from origin.
Did the electric dipole potential fall faster, slower, or the same as the point charge?
Explain the result you observed.
- For a circuit you analyzed like the one shown below
how is the voltage drop across
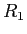 related
to the potential drop across
related
to the potential drop across  ?
Explain your observation.
?
Explain your observation.
DO NOT WRITE BELOW THIS LINE.
- Consider a situation where there is a uniform magnetic field in space that
points in the
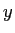 direction
direction
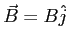 and the velocity of a particle
with charge
and the velocity of a particle
with charge 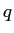 in the field is in the
in the field is in the 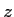 direction
direction
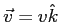 .
What is
.
What is  the angle between the magnetic field vector and the velocity vector?
What is
the angle between the magnetic field vector and the velocity vector?
What is 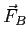 is terms of the magnitudes of
is terms of the magnitudes of 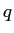 ,
, 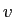 , and
, and 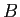 and the appropriate unit
vectors?
and the appropriate unit
vectors?
- Why is it possible for a bird to sit on a high-voltage wire without getting
electrocuted?
Problems (3). Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
18 pts. |
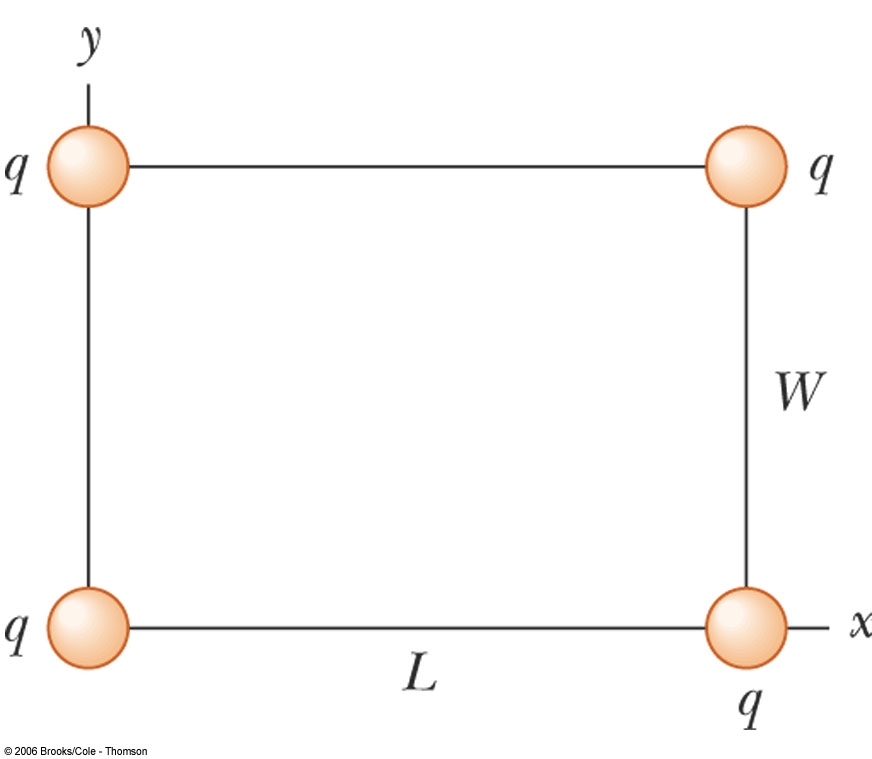
Four identical charges
are located on the corners of a rectangle as shown in the figure.
What is the total, vector electric force exerted on
the charge at the lower, right corner
in terms of 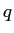 , , 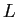 , , 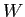 , the appropriate unit vectors, and any other necessary constants? , the appropriate unit vectors, and any other necessary constants?
|
DO NOT WRITE BELOW THIS LINE.
| 2. |
18 pts. |
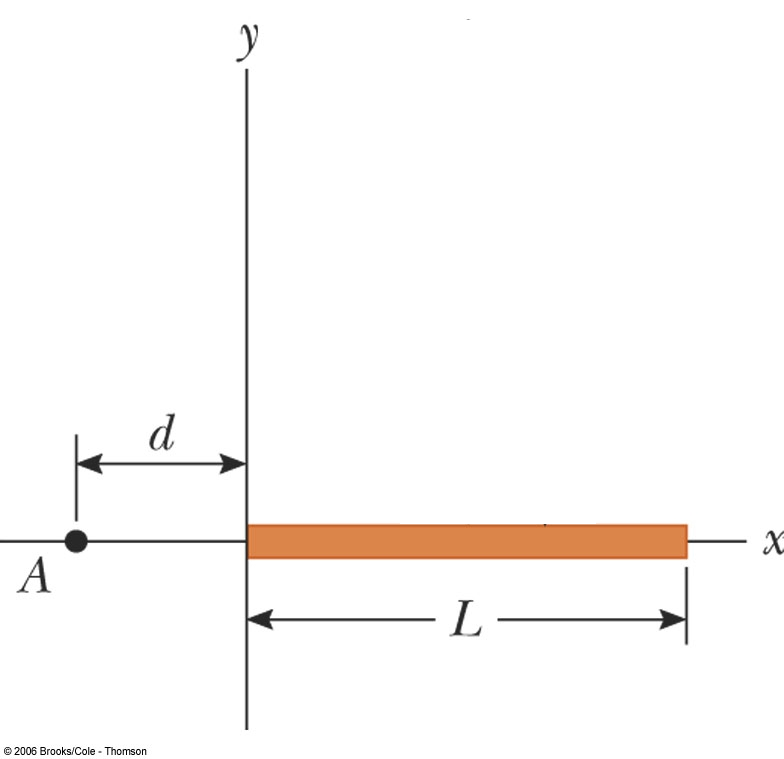
A rod of length 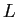 (see figure) lies along the (see figure) lies along the 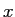 axis with its left
end at the origin.
It has a nonuniform charge density axis with its left
end at the origin.
It has a nonuniform charge density
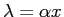 , where , where 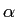 is a positive
constant.
What is the electric potential at is a positive
constant.
What is the electric potential at 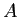 in terms of in terms of 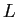 , , 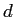 , , 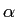 , and any other necessary
constants? , and any other necessary
constants?
|
| 3. |
24 pts. |
A proton (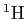 , , 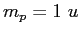 , , 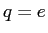 ), a deuteron ( ), a deuteron (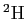 , , 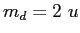 , , 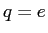 ),
and a ),
and a 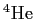 nucleus ( nucleus (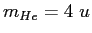 , , 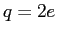 )
with the same kinetic energies enter a region of uniform magnetic field )
with the same kinetic energies enter a region of uniform magnetic field 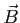 moving
perpendicular to moving
perpendicular to 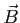 .
What is the ratio of their radii in the magnetic field? .
What is the ratio of their radii in the magnetic field?
|
Physics 132-4 Constants
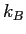 |
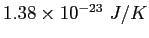 |
proton/neutron mass |
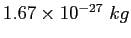 |
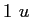 |
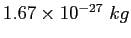 |
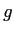 |
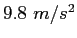 |
| Gravitation constant |
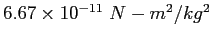 |
Earth's radius |
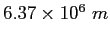 |
Coulomb constant (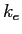 ) ) |
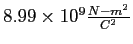 |
Electron mass |
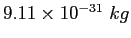 |
Elementary charge (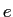 ) ) |
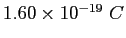 |
Proton/Neutron mass |
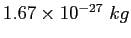 |
Permittivity constant (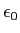 ) ) |
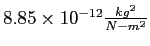 |
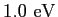 |
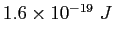 |
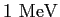 |
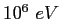 |
atomic mass unit (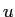 ) ) |
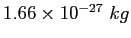 |
Physics 132-4 Equations
=100000
=2.5in
The algebraic sum of the potential changes across
all the elements of a closed loop is zero.
The sum of the currents entering a junction
is equal to the sum of the currents leaving the
junction.
The Periodic Chart.