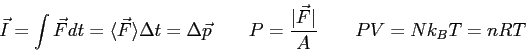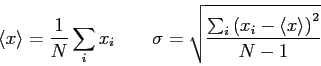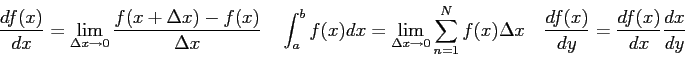Physics 132-04 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 for 8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Consider a mass of ice that is being heated.
What is the relationship between the temperature and the added heat
after the ice has melted, but before the water begins to boil?
- You pour a mass
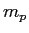 of unknown pellets at a temperature
of unknown pellets at a temperature 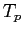 into an aluminum calorimeter cup of mass
into an aluminum calorimeter cup of mass  .
The calorimeter cup contain a mass
.
The calorimeter cup contain a mass  of water and a small mass
of water and a small mass 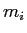 of ice.
The system comes to equilibrium at a final temperature
of ice.
The system comes to equilibrium at a final temperature 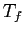 .
You can look up the specific heats of the known components of the measurement.
Write the full heat equation for the system.
Is there enough information to determine the specific heat of the pellets?
Explain.
.
You can look up the specific heats of the known components of the measurement.
Write the full heat equation for the system.
Is there enough information to determine the specific heat of the pellets?
Explain.
- In our development of kinetic theory we claimed that on average
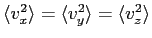 for a large number of particles in a box. Why?
for a large number of particles in a box. Why?
DO NOT WRITE BELOW THIS LINE.
- The figure shows the entropy of two solids
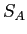 and
and 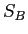 and their
combined entropy
and their
combined entropy 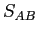 as a function of the internal energy in solid A
as a function of the internal energy in solid A 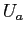 .
The solids are in thermal contact.
At the most probable macrostate we showed that
.
The solids are in thermal contact.
At the most probable macrostate we showed that
and we require that  at thermal equilibrium.
Make a guess about the relationship between
at thermal equilibrium.
Make a guess about the relationship between 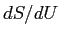 and the temperature
and the temperature 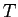 .
Justify your choice.
.
Justify your choice.
- There are two types of electric charge - positive and negative.
How did the behavior of the electroscope show this?
Problems (3). Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
12 pts. |
What is the magnitude and direction of the electric field that will balance
the weight of a proton? The proton has a charge of 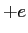 . .
|
| 2. |
15 pts. |
A spherical balloon of volume 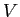 contains helium at a pressure contains helium at a pressure  .
How many atoms of helium are in the balloon if the average kinetic energy
of the helium atoms is .
How many atoms of helium are in the balloon if the average kinetic energy
of the helium atoms is
 ? Your answer should be in terms
of ? Your answer should be in terms
of  , , 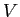 , and , and
 . .
|
Physics 132-4 Equations and Constants
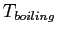 ( ( ) ) |
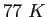 |
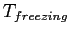 ( ( ) ) |
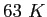 |
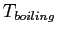 (water) (water) |
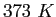 or or
 |
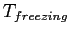 (water) (water) |
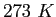 or or 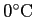 |
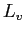 (water) (water) |
 |
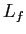 (water) (water) |
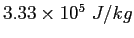 |
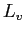 ( ( ) ) |
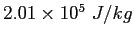 |
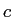 (copper) (copper) |
 |
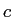 (water) (water) |
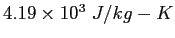 |
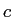 (steam) (steam) |
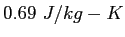 |
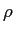 (water) (water) |
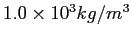 |
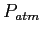 |
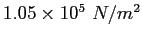 |
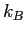 |
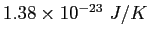 |
proton/neutron mass |
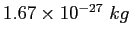 |
 |
 |
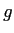 |
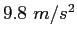 |
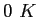 |
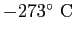 |
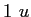 |
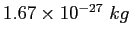 |
| Gravitation constant |
 |
Earth's radius |
 |
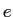 electronic charge electronic charge |
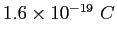 |
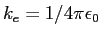 |
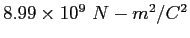 |
Physics 132-4 Equations and Constants
f 
number of degrees of freedom
The Periodic Chart.