Physics 132-2 Test 3


I pledge that I have neither given nor received unauthorized assistance during the completion of this work.


Signature height0pt depth1pt width3in


Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

  1. Consider a situation where the magnetic field in a mass spectrometer is uniform in space and points in the $z$ direction $\vec B = B \hat k$ and the velocity of the positively charged particle is in the $y$ direction $\vec v = v \hat j$. What is the $z$ component of its trajectory?

  2. The differential equation that describes nuclear decay is

    \begin{displaymath} \frac{dN_{nuc}}{dt} = -\lambda N_{nuc} \end{displaymath}

    where $N_{nuc}$ is the number of decaying nuclei and $\lambda$ is a constant characteristic of a particular nucleus. It is claimed the solution for this differential equation is

    \begin{displaymath} N_{nuc} (t) = N_0 e^{-\lambda t} \qquad . \end{displaymath}

    Prove or disprove this statement. Clearly show your method.

  3. What is the ultimate source of any magnetic field?

  4. Pushing the North pole of a magnetic toward a coil of wire induces a negative voltage in the coil. What will be the sign of the voltage if you pull the South pole of the same magnet away from the coil? Explain.

  5. In our study of double-slit interference we used a red laser to create an interference pattern like the one shown below. How would that pattern change if we used white light instead? Explain.

  6. Consider the figure in the previous question of a double-slit interference pattern. We predicted the intensity peaks should all be the same height, but that is not what we observed. Why? Explain.








Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1. 15 pts. The half-life of a particular radioactive isotope is 6.5 h. If there are initially 48 x 10\( ^{19} \) atoms of this isotope, how many atoms of this isotope remain after 26 h?

2. 17 pts. A singly-charged positive ion has a mass $m=6.4\times 10^{-26}~kg$. After being accelerated from rest through an electric potential difference $V=1000~V$, the ion enter a magnetic field of $\vert\vec B\vert = 2.0~T$ along a direction perpendicular to the direction of the field. Starting from Newton's Second Law ( $\vec F = m \vec a$), what is the radius $r$ of the path of the ion in the field?

3. 20 pts. Wire manufacturers use lasers to continually monitor the thickness of their product. The wire intercepts the laser beam producing a diffraction pattern like that of a single slit of the same width as the wire diameter. Suppose a helium-neon laser (wavelength $\lambda = 6328 \rm\AA$) illuminates a wire and the diffraction pattern is detected by a light sensor a distance $D = 2.6~m$ away. If the desired wire diameter is $a=0.02~mm$, then what is the observed distance between the two tenth-order minima (one on each side of the central maximum)? Is the small-angle approximation appropriate here? Explain.



\includegraphics[height=1.5in]{f2a.eps}





Some constants and conversion factors.

$\rho$ (water) $1.0\times 10^3 kg/m^3$ $P_{atm}$ $1.05\times 10^5 ~N/m^2$
$1.38\times 10^{-23}~J/K$ Speed of light ($c$) $3.0\times 10^{8}~m/s$
$R$ $8.31J/K-mole$ $g$
$0~K$ $\rm -273^\circ~C$ $1.67\times 10^{-27}~kg$
Gravitation constant ($G$) Earth's radius $6.37\times 10^6~m$
Coulomb constant ($k_e$) $8.99\times 10^{9} {N-m^2 \over C^2}$ Electron mass $9.11\times 10^{-31}~kg$
Elementary charge () $1.60\times 10^{-19}~C$ Proton/Neutron mass $1.67\times 10^{-27}~kg$
Permittivity constant ($\epsilon_0$) $8.85\times 10^{-12} {kg^2\over N-m^2}$ $\rm 1.0~eV$ $1.6\times 10^{-19}~J$
$\rm ^4 He$ mass $6.68 \times 10^{-27}~kg$ $\rm ^4 He$ charge $ 3.2\times 10^{-19}~C$
$\rm 1 ~MeV$ $10^6 ~ eV$

Physics 132-2 Equations







\begin{displaymath} y = A \cos (kx - \omega t) \quad k\lambda = 2 \pi \quad \om... ...ad B = B_m \sin (kx - \omega t) \quad I \propto {Amplitude}^2 \end{displaymath}


\begin{displaymath} I = 4 I_0 \cos^2 \left ( {\pi d \over \lambda} \sin \theta \... ... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2 \end{displaymath}





\begin{displaymath} {d \over dx}(x^n) = nx^{n-1} \qquad {d \over dx}(f(u)) = {df... ... du}{du \over dx} \qquad \int x^n dx = {x^{n+1} \over n+1} + c \end{displaymath}


\begin{displaymath} {d \over dx} (\cos ax) = -a\sin ax \qquad {d \over dx} (\sin ax) = a\cos ax \qquad \frac{d e^x}{dx} = e^x \end{displaymath}


\begin{displaymath} KE_0 + PE_0 = KE_1 + PE_1 \quad KE = {1 \over 2} m v^2 \quad... ...uad F_g = mg \quad \vec p_0 = \vec p_1 \quad \vec p = m \vec v \end{displaymath}


\begin{displaymath} x = \frac{a}{2} t^2 + v_0 t + x_0 \qquad v = at + v_0 \end{displaymath}


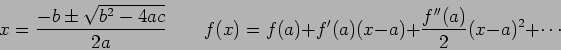
\begin{displaymath} x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \qquad f(x) = f(a) + ... ...rime (a) (x-a) + \frac{f^{\prime\prime}(a)}{2}(x-a)^2 + \cdots \end{displaymath}


\begin{displaymath} (a + b)^n = a^n + \frac{n}{1!}a^{n-1}b + \frac{n(n-1)}{2!}a^{n-2}b^2 + \cdots \end{displaymath}


\begin{displaymath} \int \frac{1}{\sqrt{x^2 + a^2}} dx = \ln \left [ x + \sqrt{x... ...] \qquad \int \frac{x}{\sqrt{x^2 + a^2}} dx = \sqrt{x^2 + a^2} \end{displaymath}


\begin{displaymath} \int \frac{x^2}{\sqrt{x^2 + a^2}} dx = \frac{1}{2} x \sqrt... ...rac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \qquad \end{displaymath}