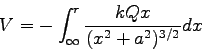
What factors in the integrand can be pulled out in front of the integral? Explain.

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (9 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
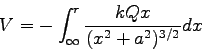

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 15 pts. | An object having a net charge
|
| 2. | 20 pts. | An accelerator produces a beam of
|
| 3. | 20 pts. | You are a summer research student at a medical-school lab that uses proton beams to treat
cancer patients.
The protons exit the machine with a speed
|
Some constants and conversion factors.
|
|
|
|
|
|
|
|
Speed of light ( |
|
|
|
|
|
|
|
|
|
|
|
|
Gravitation constant ( |
|
Earth's radius |
|
|
Coulomb constant ( |
|
Electron mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Permittivity constant ( |
|
|
|
|
|
|
|
|
|
|
|
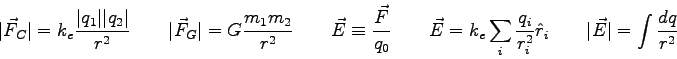


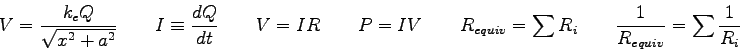
=100000
=2.5in The algebraic sum of the potential changes across all the elements of a closed loop is zero. The sum of the currents entering a junction is equal to the sum of the currents leaving the junction.

![\begin{displaymath}
\int \frac{x^2}{\sqrt{x^2 + a^2}} dx =
\frac{1}{2} x \sqrt...
...rac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \qquad
\end{displaymath}](img62.png)