Physics 132-2 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Recall the laboratory on Galilean relativity.
A projectile was fired from a toy cannon sitting on a cart that was moving horizontally.
For the horizontal component of the projectile's motion,
what is the relationship between the stationary reference frame (
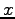 ) and the
frame of reference moving along with the cart (
) and the
frame of reference moving along with the cart (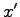 )?
Clearly explain the components of the relationship.
)?
Clearly explain the components of the relationship.
- Consider a container of water with ice added to it and placed on a heater.
What is the relationship between the temperature
and the added heat after the ice has melted, but before the water begins to boil?
What is your evidence?
- We measured the heat of vaporization of nitrogen by measuring the rate of the mass
loss from a cup of liquid nitrogen hanging from a force sensor as a small resistor heated the liquid.
We also measured the mass loss with no current in the resistor before and after we made the
measurements of the mass loss with the resistor turned on. Why?
- Recall the laboratory on the kinetic theory of ideal gases where you calculated
the specific heat of an ideal gas.
We claimed this calculation supported the atomic theory.
How?
- Consider the plot below of the entropy of two Einstein solids
 (green) and
(green) and 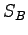 (blue)
and their
combined entropy
(blue)
and their
combined entropy 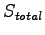 (red) plotted as a function of the number of energy
quanta
(red) plotted as a function of the number of energy
quanta 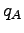 in solid
in solid 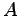 .
On the plot label the equilibrium state of the combined Einstein solids.
Explain your choice.
.
On the plot label the equilibrium state of the combined Einstein solids.
Explain your choice.
![\includegraphics[height=1.5in]{f1.eps}](img98.png)
- Find some equipotential surfaces for the electric dipole charge
configuration shown below.
Explain your method for finding the equipotentials.
![\includegraphics[height=1.25in]{f2.eps}](img99.png)
- Identify a point on the figure below where the magnetic field is
zero. Explain how you picked the point.
![\includegraphics[height=1.25in]{f3.eps}](img100.png)
- Consider some results from our laboratory on radiocarbon dating.
The table shows the number of counts and the uncertainty
for different types of radiation and different types of shielding.
Which type of radiation is most penetrating? Why?
| Radiation |
Air |
Plastic |
Lead |
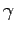 |
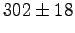 |
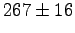 |
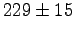 |
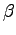 |
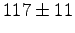 |
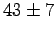 |
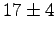 |
 |
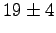 |
 |
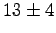 |
- If you hold two flashlights close together will you see an interference pattern?
Explain.
- What happens to the width of the central maximum of a single-slit diffraction pattern
as the width of the slit is made narrower?
Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
5 pts. |
How fast must a meter stick be moving if its length is measured to shrink to 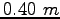 ? ?
|
| 2. |
7 pts. |
The fraternal twins Xena and Thor join a migration from Earth to Planet 10.
Planet 10 is a distance 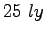 away in an inertial reference frame at rest with respect
to both planets.
The twins of the same age depart at the same time on different spaceships.
Xena's ship has a speed away in an inertial reference frame at rest with respect
to both planets.
The twins of the same age depart at the same time on different spaceships.
Xena's ship has a speed  while Thor travels at while Thor travels at 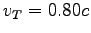 .
What is the age difference between the twins when Thor arrives at Planet 10?
Which twin is older? .
What is the age difference between the twins when Thor arrives at Planet 10?
Which twin is older?
|
| 3. |
8 pts. |
An electron is released from rest on the axis of a uniformly charged ring a distance
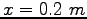 from the center of the ring.
If the linear charge density of the ring is from the center of the ring.
If the linear charge density of the ring is
 and the
radius of the ring is and the
radius of the ring is 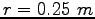 ,
what is the potential energy of the electron at the moment of release? ,
what is the potential energy of the electron at the moment of release?
|
| 4. |
10 pts. |
A newly-created material has a multiplicity
where 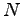 is the number of atoms in the solid, is the number of atoms in the solid,
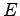 is the total, internal energy in the solid, and is the total, internal energy in the solid, and  and and  are constants of
proportionality.
(a) How does the temperature of the new material depend on the internal energy?
(b) What is the molar heat capacity for this solid? are constants of
proportionality.
(a) How does the temperature of the new material depend on the internal energy?
(b) What is the molar heat capacity for this solid?
|
Some constants and conversion factors.
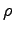 (water) (water) |
 |
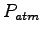 |
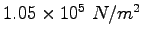 |
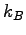 |
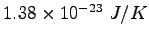 |
Speed of light (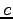 ) ) |
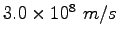 |
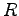 |
 |
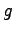 |
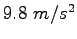 |
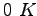 |
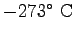 |
 |
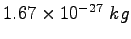 |
Gravitation constant (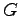 ) ) |
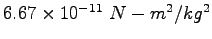 |
Earth's radius |
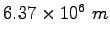 |
Coulomb constant (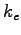 ) ) |
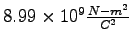 |
Earth's mass |
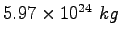 |
Elementary charge (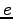 ) ) |
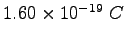 |
Proton/Neutron mass |
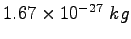 |
Permittivity constant ( ) ) |
 |
Electron mass |
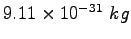 |
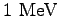 |
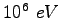 |
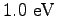 |
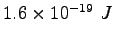 |
Physics 132-2 Equations
f 
number of degrees of freedom
=100000
=2.5in
The algebraic sum of the potential changes across
all the elements of a closed loop is zero.
The sum of the currents entering a junction
is equal to the sum of the currents leaving the
junction.
![\includegraphics[height=1.5in]{f1.eps}](img98.png)
![\includegraphics[height=1.25in]{f2.eps}](img99.png)
![\includegraphics[height=1.25in]{f3.eps}](img100.png)
![\includegraphics[height=1.5in]{f1.eps}](img98.png)
![\includegraphics[height=1.25in]{f2.eps}](img99.png)
![\includegraphics[height=1.25in]{f3.eps}](img100.png)

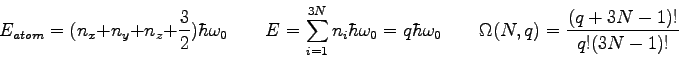
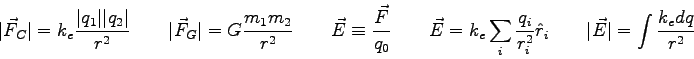
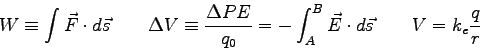


![\begin{displaymath}
I = 4 I_0 \cos^2 \left ( {\pi d \over \lambda} \sin \theta \...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img87.png)


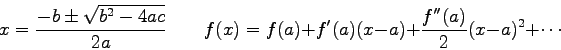
![\begin{displaymath}
\int \frac{x^2}{\sqrt{x^2 + a^2}} dx =
\frac{1}{2} x \sqrt...
...rac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \qquad
\end{displaymath}](img96.png)