Physics 132-1 Test 3
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- The position of two-slit interference maxima can be described by
where 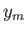 is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and
is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and 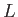 is
the distance from the slits to the phototransistor. The quantity
is
the distance from the slits to the phototransistor. The quantity  is the slit separation,
is the slit separation,  is the wavelength of the light,
and
is the wavelength of the light,
and 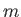 is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
- Consider this question about oscillating charges.
Suppose the motion of the charges can be described as an oscillating dipole so the
dipole moment as a function of time looks like the figure below.
Assume the dipole is aligned with the
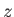 -axis.
What do you expect the electric field to look like as a function of time
at some arbitrary distance
-axis.
What do you expect the electric field to look like as a function of time
at some arbitrary distance 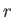 away from the source in the
away from the source in the 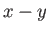 plane?
What is the direction of the
plane?
What is the direction of the  field?
Make a sketch of your answer on the plot and label your curve.
field?
Make a sketch of your answer on the plot and label your curve.
- The decay of atomic nuclei is often characterized by a quantity
known as the half-life
 . The half-life is the period of
time for one-half of the original sample to disappear via radioactive
decay. This statement can be expressed mathematically as
. The half-life is the period of
time for one-half of the original sample to disappear via radioactive
decay. This statement can be expressed mathematically as
 .
Starting with this expression show that the decay constant
.
Starting with this expression show that the decay constant  and the half-life are related by the following equation.
and the half-life are related by the following equation.
- The intensity
pattern due to diffraction of light passing through a single slit is
where 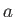 is the size of the single slit,
is the size of the single slit, 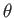 is the angular
position of the light,
is the angular
position of the light, 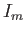 is the maximum intensity at the center,
and
is the maximum intensity at the center,
and  is the wavelength of the light. The shape is shown in the figure below.
Generate an expression for the angular width of the central
maximum in terms of
is the wavelength of the light. The shape is shown in the figure below.
Generate an expression for the angular width of the central
maximum in terms of 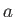 ,
,  , and any other constants you
need.
, and any other constants you
need.
![\includegraphics[height=1.5in]{diffraction_of_light_fig_3.eps}](img76.png)
- If the mass of a radioactive sample is doubled, do the activity of the sample and the decay constant increase,
decrease, or stay the same.
Explain.
- In lab we used a red laser to observe two-slit interference. Would the experiment
work if we used white light?
Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
A beam of bright laser light of wavelength
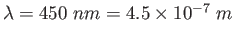 passes through a diffraction
grating. Enclosing the space beyond the grating is a large screen forming a half-cylinder centered on
the grating with the cylinder's axis parallel to the slits in the grating.
Eleven bright spots appear on the screen.
What are the maximum and minimum values of the slit separation in the diffraction grating? passes through a diffraction
grating. Enclosing the space beyond the grating is a large screen forming a half-cylinder centered on
the grating with the cylinder's axis parallel to the slits in the grating.
Eleven bright spots appear on the screen.
What are the maximum and minimum values of the slit separation in the diffraction grating?
|
Physics 132-1 Constants
 (water) (water) |
 |
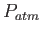 |
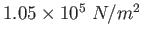 |
 |
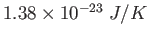 |
proton/neutron mass |
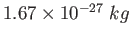 |
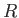 |
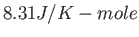 |
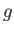 |
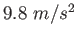 |
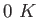 |
 |
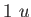 |
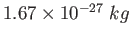 |
| Gravitation constant |
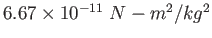 |
Earth's radius |
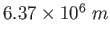 |
Coulomb constant (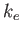 ) ) |
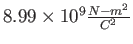 |
Electron mass |
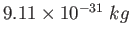 |
Elementary charge (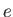 ) ) |
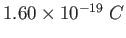 |
Proton/Neutron mass |
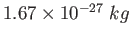 |
Permittivity constant ( ) ) |
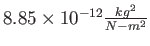 |
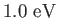 |
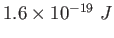 |
 mass mass |
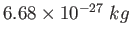 |
 charge charge |
 |
 |
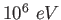 |
Earth-Moon distance |
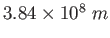 |
Premeability constant (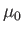 ) ) |
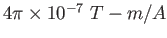 |
Speed of Light ( ) ) |
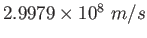 |
Physics 132-1 Equations
![]() is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and
is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and ![]() is
the distance from the slits to the phototransistor. The quantity
is
the distance from the slits to the phototransistor. The quantity ![]() is the slit separation,
is the slit separation, ![]() is the wavelength of the light,
and
is the wavelength of the light,
and ![]() is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
![\includegraphics[height=2.0in]{induction3fig1.eps}](img11.png)
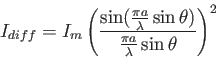
![]() is the size of the single slit,
is the size of the single slit, ![]() is the angular
position of the light,
is the angular
position of the light, ![]() is the maximum intensity at the center,
and
is the maximum intensity at the center,
and ![]() is the wavelength of the light. The shape is shown in the figure below.
Generate an expression for the angular width of the central
maximum in terms of
is the wavelength of the light. The shape is shown in the figure below.
Generate an expression for the angular width of the central
maximum in terms of ![]() ,
, ![]() , and any other constants you
need.
, and any other constants you
need.
![\includegraphics[height=1.5in]{diffraction_of_light_fig_3.eps}](img76.png)
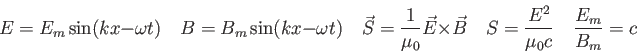
![\begin{displaymath}
I = \frac{E^2}{2\mu_0 c} = 2\rho_{EM} c \quad
I = 4 I_0 \cos...
...a \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2 \quad
\end{displaymath}](img66.png)
![\begin{displaymath}
I = I_m \cos^2 \left ( {\pi d \over \lambda} \sin \theta \ri...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img67.png)
![\begin{displaymath}
\int \frac{x^2}{\sqrt{x^2 + a^2}} dx =
\frac{1}{2} x \sqrt...
...rac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \qquad
\end{displaymath}](img75.png)