Physics 132-1 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- How can an electroscope be used to determine the charge of an object?
- Consider the field lines of an electric dipole shown in the figure.
What do the equipotentials look like? Draw a representative set of equipotentials
and state clearly what guided you in your drawing.
![\includegraphics[height=1.5in]{dipole1.ps}](img70.png)
- In lab, you were asked to calculate the electric field of the ring with total charge
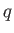 like the one shown in the
figure by starting from
the electric field of a point charge and integrating over the charge distribution.
In the course of that calculation you encountered the following
integral
like the one shown in the
figure by starting from
the electric field of a point charge and integrating over the charge distribution.
In the course of that calculation you encountered the following
integral
where 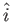 is the unit vector in the
is the unit vector in the 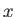 direction,
direction,  is the radius of the ring,
is the radius of the ring, 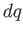 is
an infinitesimal piece of charge on the ring,
is
an infinitesimal piece of charge on the ring, 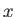 is the position along the axis in the figure, and
is the position along the axis in the figure, and
 is the Coulomb constant.
Calculate this integral and explain your steps.
is the Coulomb constant.
Calculate this integral and explain your steps.
![\includegraphics[height=1.5in]{electric_potential_fig_6.eps}](img71.png)
- Can the resistance of a series combination of electrical resistors ever be less than
the resistance of the largest resistor? Explain.
- Consider the
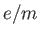 experiment where you measured the mass of the electron. You generated
the equation
experiment where you measured the mass of the electron. You generated
the equation
where 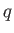 is the electronic charge,
is the electronic charge, 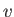 is the electron speed,
is the electron speed,  is the magnitude of the magnetic field,
is the magnitude of the magnetic field,
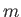 is the electron mass, and
is the electron mass, and 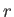 is the radius of the electron's trajectory.
Where does the left-hand side of the equation come from?
Where does the right-hand side of the equation come from?
is the radius of the electron's trajectory.
Where does the left-hand side of the equation come from?
Where does the right-hand side of the equation come from?
- Consider the following idea for a novel propulsion for a ship or submarine.
In this `magnetohydrodynamic drive' seawater flows between the poles of a magnet as shown below and
an electric field drives a current through
the seawater.
The magnetic force on this current propels
the water towards the rear of the ship pushing the ship
forward.
What should be the direction of the applied electric field in the
region between the poles of the magnet?
Explain.
Movie buffs might recognize this drive from the 1990 movie Hunt for Red October starring Sean Connery.
![\includegraphics[height=1.0in]{RedOctober.eps}](img72.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
When the two Apollo astronauts were on the surface of the Moon, a third astronaut
orbited the Moon.
Assume the third astronaut's orbit to be circular and
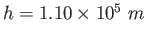 above the surface of the Moon.
At this altitude the free-fall acceleration of the Moon's gravity is above the surface of the Moon.
At this altitude the free-fall acceleration of the Moon's gravity is
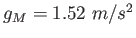 .
The Moon's radius is .
The Moon's radius is
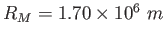 .
What is the third astronaut's orbital speed? .
What is the third astronaut's orbital speed? |
Physics 132-1 Constants
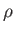 (water) (water) |
 |
 |
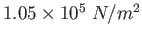 |
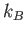 |
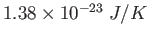 |
proton/neutron mass |
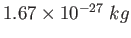 |
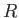 |
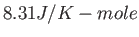 |
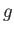 |
 |
 |
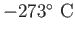 |
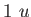 |
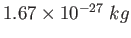 |
| Gravitation constant |
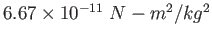 |
Earth's radius |
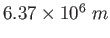 |
Coulomb constant ( ) ) |
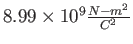 |
Electron mass |
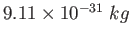 |
Elementary charge (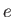 ) ) |
 |
Proton/Neutron mass |
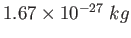 |
Permittivity constant (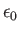 ) ) |
 |
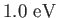 |
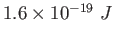 |
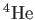 mass mass |
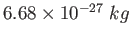 |
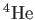 charge charge |
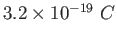 |
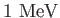 |
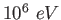 |
|
|
Physics 132-1 Equations
=100000
=2.5in
The algebraic sum of the potential changes across
all the elements of a closed loop is zero.
The sum of the currents entering a junction
is equal to the sum of the currents leaving the
junction.
![\includegraphics[height=1.5in]{dipole1.ps}](img70.png)
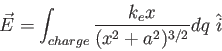
![\includegraphics[height=1.5in]{electric_potential_fig_6.eps}](img71.png)
![\includegraphics[height=1.0in]{RedOctober.eps}](img72.png)
![\includegraphics[height=1.5in]{dipole1.ps}](img70.png)
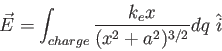
![\includegraphics[height=1.5in]{electric_potential_fig_6.eps}](img71.png)
![\includegraphics[height=1.0in]{RedOctober.eps}](img72.png)
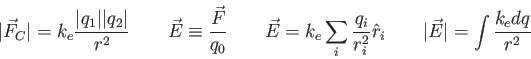

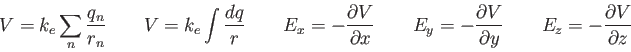

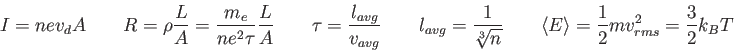
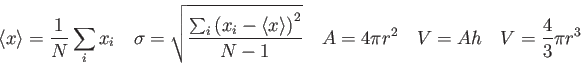
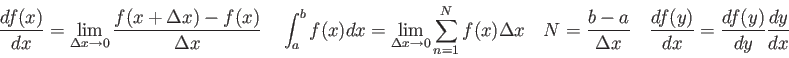
![\begin{displaymath}
\int \frac{x^2}{\sqrt{x^2 + a^2}} dx =
\frac{1}{2} x \sqrt...
...rac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \qquad
\end{displaymath}](img69.png)