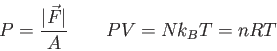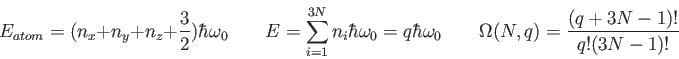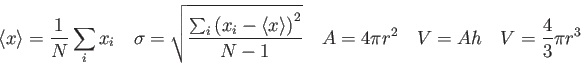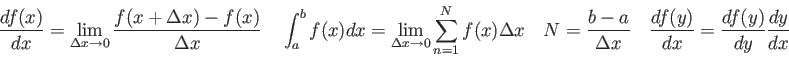Physics 132-1 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- We claim that matter consists of atoms and molecules.
What evidence can you cite to support that claim?
- A series of measurements of the pressure-temperature
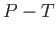 relationship of a gas
at constant volume are made and found to lie along a line.
Extrapolating to the point where
relationship of a gas
at constant volume are made and found to lie along a line.
Extrapolating to the point where 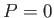 yields the value of absolute zero.
The average and standard deviation of the series is
yields the value of absolute zero.
The average and standard deviation of the series is
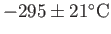 .
Is this result consistent with the expected value of -273? Explain.
.
Is this result consistent with the expected value of -273? Explain.
- Consider the following results from the kinetic theory
where 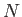 is the number of particles in a gas,
is the number of particles in a gas,  is the temperature,
and
is the temperature,
and
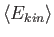 is the average energy for a particle in the
gas.
Starting with these results show the following.
Clearly show all your steps.
is the average energy for a particle in the
gas.
Starting with these results show the following.
Clearly show all your steps.
- Consider a gas in a container. Would it violate Newton's Laws or any other physical law
if all the particles in the gas collided in such a way that all of the gas particles
ended up in the bottom half of the container leaving the top half empty? Is such a scenario likely? Explain.
- The plot below has the results of a calculation of the multiplicities of an Einstein solid with
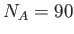 ,
, 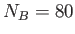 , and
, and 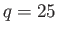 .
What is the width of the probability distribution? What is the most probable energy in terms of
.
What is the width of the probability distribution? What is the most probable energy in terms of 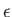 ,
the energy quantum? Show your reasoning for full credit.
,
the energy quantum? Show your reasoning for full credit.
![\includegraphics[height=2.75in]{statmech1.eps}](img69.png)
- The force exerted by a gas on the walls of a container is constant in time (think about a balloon).
Someone challenging the atomic picture of gases claims that you should see fluctuations in the
pressure exerted on the walls like the fluctuations in the motion of small particles observed in Brownian motion.
How would you respond?
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
Physics 132-2 Equations and Constants
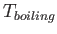 ( (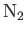 ) ) |
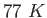 |
 ( (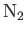 ) ) |
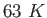 |
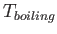 (water) (water) |
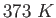 or or
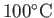 |
 (water) (water) |
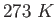 or or  |
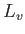 (water) (water) |
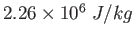 |
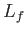 (water) (water) |
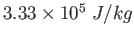 |
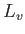 ( (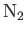 ) ) |
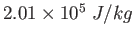 |
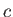 (copper) (copper) |
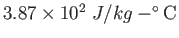 |
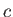 (water) (water) |
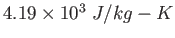 |
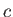 (steam) (steam) |
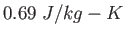 |
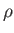 (water) (water) |
 |
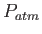 |
 |
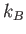 |
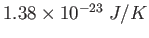 |
proton/neutron mass |
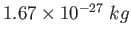 |
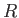 |
 |
 |
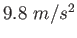 |
 |
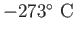 |
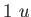 |
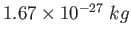 |
| Gravitation constant |
 |
Earth's radius |
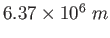 |
![\includegraphics[height=2.75in]{statmech1.eps}](img69.png)
![\includegraphics[height=2.75in]{statmech1.eps}](img69.png)