Physics 132-1 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (4 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- If one writes the equation for the Balmer series for two different
spectral lines - once, say for the
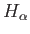 wavelength
wavelength
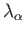 ,
and once for the
,
and once for the 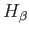 wavelength,
wavelength,  , then one can eliminate
, then one can eliminate 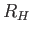 :
:
How can you estimate the value of the three 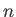 values in the previous equation?
values in the previous equation?
- Consider the plot below of the effective potential for a macroscopic particle (blue curve)
and its line of constant energy (red curve).
Describe the motion of the particle in this potential.
What restrictions are there on the energy
 of a classical particle?
of a classical particle?
![\includegraphics[height=1.5in]{f1.eps}](img104.png)
- Recall the rotational collision of a rotating disk and a cylindrical weight dropped onto the disk.
Come up with a formula for the rotational inertia,
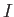 , of the whole system
before and after the collision in terms of
, of the whole system
before and after the collision in terms of 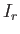 the moment of inertia of the rotator,
the moment of inertia of the rotator,
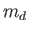 and
and  the mass and radius of the disk,
the mass and radius of the disk, 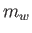 and
and 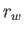 the mass and radius of the
weight dropped on the disk, and
the mass and radius of the
weight dropped on the disk, and 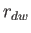 the distance from the center of the disk to the center of
the weight.
the distance from the center of the disk to the center of
the weight.
- In solving the Schroedinger equation what requirement or postulate forces us to choose particular energy
states
(i.e. what causes energy quantization)?
- Consider what happens when two Einstein solids come in contact.
The number of atoms for solid
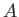 is
is  it contains two quanta of energy so
it contains two quanta of energy so 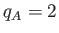 .
Let
.
Let 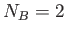 (two whole atoms!) and
(two whole atoms!) and 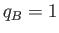 .
Now bring the your solids
.
Now bring the your solids 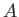 and
and 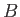 `together' into a single system.
What is the total multiplicity
`together' into a single system.
What is the total multiplicity 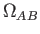 for the combined system
with
for the combined system
with 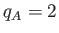 and
and 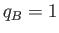 in its initial macrostate?
in its initial macrostate?
- Consider a container of water with ice added to it and placed on a heater.
What is the relationship between the temperature and the added heat after the ice has melted,
but before the water begins to boil? What is your evidence?
- How does a mass spectrometer work?
- Consider the plot below showing equipotentials for the charges in the figure
(filled circles are negative, open circles are positive).
Draw a full set of of electric field lines with appropriate directions to accompany the equipotentials.
Explain your reasoning.
![\fbox{\includegraphics[height=1.25in]{charges2.eps}}](img23.png)
- Consider the measured intensity pattern from a pair of narrow slits of width
 separated
by a distance
separated
by a distance 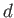 . How would you determine
. How would you determine  if
if 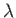 is known?
is known?
![\includegraphics[height=1.5in]{diffractionF4.eps}](img105.png)
- Can radiocarbon dating be used to measure the age of very old (about a billion years) material?
- Consider a solid cube made of a good conductor, i.e. a metal.
If charge is added to the cube where will it be located at equilibrium? Explain.
- Two rooms of equal volume are connected by an open passageway, but are maintained at different temperatures.
Does each room have the same number of air molecules? Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
6 pts. |
What is the energy of the hydrogen atom electron whose probability density
for 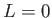 is represented by the plot shown below?
What minimum energy is needed to remove this electron from the atom? is represented by the plot shown below?
What minimum energy is needed to remove this electron from the atom?
|
| 2. |
8 pts. |
Imagine that a particle has a wave function
What is the probability the particle will be found in the range 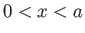 ? ?
|
| 3. |
8 pts. |
The liquid-drop model of the atomic nucleus predicts that high-energy
oscillations of certain nuclei can split the nucleus into two unequal fragments and
a few neutrons.
The fission products acquire kinetic energy from their mutual Coulomb repulsion.
Calculate the electric potential energy (in electron volts)
of two spherical fragments from a uranium nucleus having the following
charges and radii: 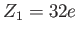 and and
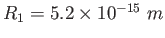 ; ; 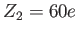 and and
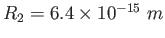 .
Assume that the charge is uniformly distributed throughout the volume of each spherical
nucleus and that just before separating each fragment is at rest and their surfaces are in
contact.
The electrons surrounding the nucleus can be ignored. .
Assume that the charge is uniformly distributed throughout the volume of each spherical
nucleus and that just before separating each fragment is at rest and their surfaces are in
contact.
The electrons surrounding the nucleus can be ignored.
|
| 4. |
10 pts. |
A newly-created material has a multiplicity
where 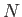 is the number of atoms in the solid, is the number of atoms in the solid,
 is the total, internal energy in the solid, and is the total, internal energy in the solid, and  is a constant of
proportionality. is a constant of
proportionality.
- How does the temperature of the new material depend on the internal energy?
- What is the molar heat capacity for this solid?
- Could this material really exist? Why or why not?
|
| 5. |
10 pts. |
The figure below shows a some data for intensity versus diffraction angle
for the diffraction of an x-ray beam through a crystal
acting like a diffraction grating.
The beam consists of two wavelengths and the spacing between the planes of atoms is 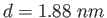 .
What are the two wavelengths? .
What are the two wavelengths?
|
Physics 132-1 Constants
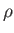 (water) (water) |
 |
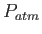 |
 |
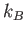 |
 |
proton/neutron mass |
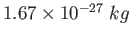 |
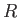 |
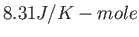 |
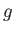 |
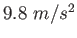 |
 |
 |
 |
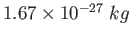 |
| Gravitation constant |
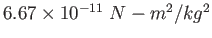 |
Earth's radius |
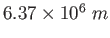 |
Coulomb constant ( ) ) |
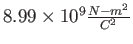 |
Electron mass |
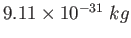 |
Elementary charge (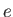 ) ) |
 |
Proton/Neutron mass |
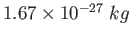 |
Permittivity constant (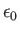 ) ) |
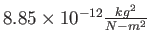 |
 |
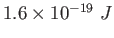 |
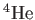 mass mass |
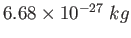 |
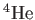 charge charge |
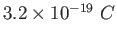 |
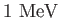 |
 |
Earth-Moon distance |
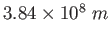 |
Premeability constant (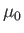 ) ) |
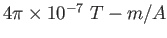 |
Speed of Light (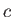 ) ) |
 |
Physics 132-1 Equations
=100000
=2.5in
The algebraic sum of the potential changes across
all the elements of a closed loop is zero.
The sum of the currents entering a junction
is equal to the sum of the currents leaving the
junction.
Moments of Inertia
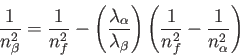
![\includegraphics[height=1.5in]{f1.eps}](img104.png)
![\fbox{\includegraphics[height=1.25in]{charges2.eps}}](img23.png)
![\includegraphics[height=1.5in]{diffractionF4.eps}](img105.png)
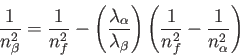
![\includegraphics[height=1.5in]{f1.eps}](img104.png)
![\fbox{\includegraphics[height=1.25in]{charges2.eps}}](img23.png)
![\includegraphics[height=1.5in]{diffractionF4.eps}](img105.png)
![\includegraphics[height=1.25in]{hydrogen1.ps}](img28.png)

![\includegraphics[height=1.5in]{diffraction2.ps}](img39.png)
![\includegraphics[height=2.0in]{charges3.eps}](img41.png)

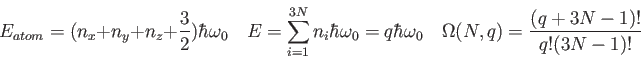
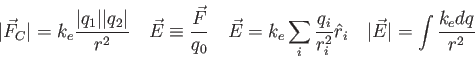

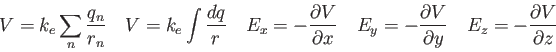
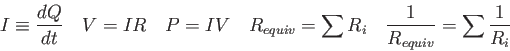


![\begin{displaymath}
I = \frac{E^2}{2\mu_0 c} = 2\rho_{EM} c \quad
I = 4 I_0 \cos...
...a \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2 \quad
\end{displaymath}](img92.png)
![\begin{displaymath}
I = I_m \cos^2 \left ( {\pi d \over \lambda} \sin \theta \ri...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img93.png)
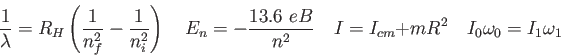
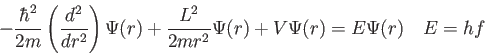
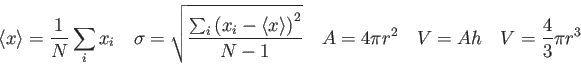
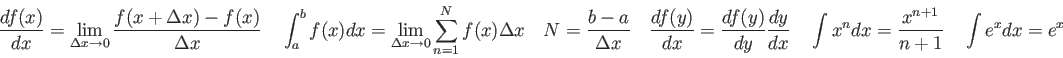
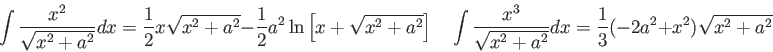
![\includegraphics[width=5.5in]{10t02a.ps}](img102.png)
![\includegraphics[width=5.5in]{10t02b.ps}](img103.png)