![]()
where ![]() is the expression describing radioactive decay.
Starting with the above expression show that the decay constant
is the expression describing radioactive decay.
Starting with the above expression show that the decay constant ![]() and the half-life are related by the following equation.
and the half-life are related by the following equation.
![\includegraphics[]{fig1.eps}](img45.png)
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
![]()
where ![]() is the expression describing radioactive decay.
Starting with the above expression show that the decay constant
is the expression describing radioactive decay.
Starting with the above expression show that the decay constant ![]() and the half-life are related by the following equation.
and the half-life are related by the following equation.
![\includegraphics[]{fig1.eps}](img45.png)
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 15 pts. | A radioactive isotope of mercury, |
| 2. | 17 pts. | Measurements are made of the intensity distribution in
a Young's, double-slit, interference pattern (see figure below).
At a particular value of
|
| 3. | 20 pts. | The Impressionist painter Georges Seurat created paintings like the
one shown below with an enormous number of dots of pure pigment, each of which
was approximately
|
Some useful constants, conversion factors, integrals, and other equations.
| Coulomb's Law constant (
|
|
Electron mass |
|
| Elementary charge ( |
|
Proton/Neutron mass |
|
| Permittivity constant ( |
|
|
|
|
|
![\begin{eqnarray*}
\int { dx \over (x^2 + a^2 )^{3/2}} = {x \over a^2(x^2 + a^2)^...
...[5pt]
\int {x dx \over x+d} = x - d\ln (x+d) \qquad & & \\ [5pt]
\end{eqnarray*}](img33.png)
![\begin{displaymath}
I = I_m \cos^2 \left ( {\pi d \over \lambda} \sin \theta \ri...
...a \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2 \quad
\end{displaymath}](img38.png)
![\begin{displaymath}
I = I_m \cos^2 \left ( {\pi d \over \lambda} \sin \theta \ri...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img39.png)
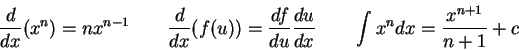
![\includegraphics[]{pertable2.eps}](img44.png)