Physics 132-2 Test 1

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. We measured in lab the latent heat of vaporization of nitrogen. What was the temperature of the liquid nitrogen during the experiment? Explain how you know this.

2. Sketch a plot of volume versus pressure for a gas. What sort of mathematical equation relates the two quantities?

   

3. How did you determine absolute zero?

4. In our model for the kinetic theory we made the assertion that $v^2_{total} = 3v^2_x$. Justify this step.

5. The table below has the results of a calculation of the multiplicities of an Einstein solid with $N_A = 100$, $N_B=100$, and $q=20$. What is the probability that all of the quanta end up in solid A? What is the width of the probability distribution? Show your reasoning for full credit.
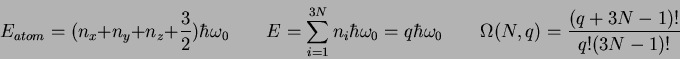
   height0pt depth1pt width5in

                                                            Fraction
   U(A)  U(B)     Omega(A)       Omega(B)      Omega(AB)    of states
   ----  ----  -------------  -------------  -------------  ---------
      0    20            1    2.664e+31      2.664e+31      1.30e-6
      1    19          300    1.670e+30      5.011e+32      2.44e-5
      2    18       45,150    9.980e+28      4.506e+33      0.00022*
      3    17    4,545,100    5.667e+27      2.576e+34      0.00125*
      4    16  344,291,325    3.049e+26      1.050e+35      0.00511*
      5    15  2.093e+10      1.549e+25      3.242e+35      0.01577*
      6    14  1.064e+12      7.398e+23      7.872e+35      0.03829*
      7    13  4.652e+13      3.309e+22      1.539e+36      0.07487*
      8    12  1.785e+15      1.379e+21      2.461e+36      0.11972*
      9    11  6.109e+16      5.320e+19      3.250e+36      0.15808*
     10    10  1.888e+18      1.888e+18      3.563e+36      0.17333*
     11     9  5.320e+19      6.109e+16      3.250e+36      0.15808*
     12     8  1.379e+21      1.785e+15      2.461e+36      0.11972*
     13     7  3.309e+22      4.652e+13      1.539e+36      0.07487*
     14     6  7.398e+23      1.064e+12      7.872e+35      0.03829*
     15     5  1.549e+25      2.093e+10      3.242e+35      0.01577*
     16     4  3.049e+26      344,291,325    1.050e+35      0.00511*
     17     3  5.667e+27        4,545,100    2.576e+34      0.00125*
     18     2  9.980e+28           45,150    4.506e+33      0.00022*
     19     1  1.670e+30              300    5.011e+32      2.44e-5
     20     0  2.664e+31                1    2.664e+31      1.30e-6
    
                Total number of microstates: 2.056e+37
   

6. Consider a strange solid whose multiplicity is always one ($\Omega_A=1$) no matter how much energy you put in it. If you put lots of energy in solid $A$ and then put it into thermal contact with a `normal' Einstein solid (solid $B$) that has the same number of atoms ($N_A = N_B$), but far less energy ($q_A » q_B$), what happens? Explain.

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.

15 pts.

A cube $l = 0.2 m$ on a side contains air with an equivalent molar mass $m_n = 28.9 g/mole$ at atmospheric pressure ( $P_0=1.01\times 10^5 N/m^2$) and $T=280 K$. (a) What is the mass of the gas and (b) what is the force it exerts on each face of the cube?

2.	17 pts.	An incandescent light bulb contains a fixed volume $V$ of argon at pressure $P_0$. The bulb is switched on and a constant power $\mathcal{P}_l$ is transferred to the argon for a time interval $\Delta t$. (a) Show the final pressure $P_1$ in the bulb at the end of this process is $$P_1 = P_0 \left ( 1 + \frac{\mathcal{P}_l\Delta tR}{P_0V C_V} \right ) \qquad .$$ (b) Find the pressure in the spherical bulb of diameter $d=0.08 m$ after a time $\Delta t = 8.0 s$. The power of the light bulb is $\mathcal{P}_l= 3.0 J/s$ and the initial pressure is $P_0=1.01\times 10^5 N/m^2$.
3.	20 pts.	A newly-created material has a multiplicity $$\Omega = \alpha N E$$ where $N$ is the number of atoms in the solid, $E$ is the total, internal energy in the solid, and $\alpha$ is a constant of proportionality. (a) How does the temperature of the new material depend on the internal energy? (b) What is the molar heat capacity for this solid? (c) Could this material really exist? Why or why not?

Some constants.

$T_{boiling}$ ($\rm N_2$)	$77 K$	$T_{freezing}$ ($\rm N_2$)	$63 K$
$T_{boiling}$ (water)	$373 K$ or $100^\circ\rm C$	$T_{freezing}$ (water)	$273 K$ or $0^\circ\rm C$
$L_v$(water)	$2.26\times 10^6 J/kg$	$L_f$ (water)	$3.33\times 10^5 J/kg$
$c$ (water)	$4.19\times 10^3 J/kg-K$	$c$ (steam)	$0.69 J/kg-K$
$\rho$ (water)	$1.0\times 10^3 kg/m^3$	$P_{atm}$	$1.05\times 10^5 N/m^2$
$k_B$	$1.38\times 10^{-23} J/K$	proton/neutron mass	$1.67\times 10^{-27} kg$
$R$	$8.31J/K-mole$	$g$	$9.8 m/s^2$
$0 K$	$\rm -273^\circ C$	$1  u$	$1.67\times 10^{-27} kg$
Gravitation constant	$6.67 \times 10^{-11} N-m^2/kg^2$	Earth's radius	$6.37\times 10^6 m$

Physics 132-2 Equations

$$P = {\vert\vec F\vert \over A} \qquad PV = Nk_B T = nRT \qquad F_g = mg \qquad$$

$$Q = C\Delta T = cm\Delta T = n C_v \Delta T \qquad Q_{f,v} = m L_{f,v}$$

$$\Delta E_{int} = Q+W \qquad W = \int_a^b \vec F \cdot d\vec ... ..._b} P dV \rightarrow P\Delta V \qquad W = F_{constant}d \qquad$$

$$\vec F = m \vec a = {d\vec p \over dt} \qquad \langle \vec F \rangle = {\Delta \vec p \over \Delta t} \qquad$$

$$KE = {1 \over 2} mv^2 \qquad ME_0 = ME_1 \qquad \vec p = m \vec v \qquad \vec p_0 = \vec p_1 \qquad$$

$$\overline {KE} = \langle E_{kin} \rangle = {1 \over 2}m \o... ...qquad E_{int} = N  \langle E_{kin} \rangle = {3\over 2} Nk_BT$$

$$v_{rms} = \sqrt{\overline {v^2} } \qquad C_{V} = {f\over 2} ... ...\qquad E_f = { k_BT \over 2} \qquad E_{int} = {f\over 2} Nk_BT$$

f $\equiv$ number of degrees of freedom

$$E_{atom} = (n_x + n_y + n_z + \frac{3}{2}) \hbar \omega_0 \q... ...ar \omega_0 \qquad \Omega(N,q) = \frac{(q+3N-1)!}{q! (3N-1)!}$$

$$S = k_B\ln \Omega \qquad \frac{1}{T} = \frac{dS}{dE} \qqua... ...0} \qquad C = \frac{1}{n} \frac{dE}{dT} \qquad E = 3Nk_B T$$

$${d \over dx} x^n = nx^{n-1} \qquad \int x^n dx = {x^{n+1} \o... ...{1}{x} \qquad \frac{df(u)}{dx} = \frac{df(u)}{du}\frac{du}{dx}$$

$$\ln (a\times 10^b) = \ln a + b\ln 10 \qquad e^x = 10^y \quad... ...um_i \left( x_{i}-\left\langle x\right\rangle \right)^2}{N-1}}$$

$$A = 4\pi r^2 \qquad V = Ah \qquad V = {4\over 3} \pi r^3$$