Physics 132-1 Test 2

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. What do electric field lines represent?

2. In lab you showed there was a significant gravitational attraction halfway between the Earth and the Moon. Why, then, do astronauts experience weightlessness when they are orbiting a mere 120 km above the Earth?

   
   
   
   
   
   
   
   

3. Consider the charge distribution below. What do the equipotential lines look like outside the ring and lying in the plane of the paper? What does the electric potential look like inside the ring of charge and lying in the plane of the paper? Explain your reasoning.

   
   
   
   

   

   
   
   
   

4. A particle of electric charge $q$ in a uniform electric field of magnitude $E$ follows the path in the figure . What is the work done by the field on the charge? Explain.

   
   
   

   

5. Consider the circuit shown below where $R_1 < R_2$. Which leg of the circuit carries the most current? Explain your reasoning.

   
   

   

6. The figure below shows the electric potential $V$ as a function of $x$. Which region along the $x$ axis has the largest magnitude electric field? Which region has the lowest? Explain your reasoning.

   

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.	15 pts.	In nuclear fission, atomic nuclei split into two pieces and acquire kinetic energy from the electrostatic repulsion of the two pieces. What is the electric potential energy between two spherical fragments having the following charges and radii: $q_1 = 38e$, $r_1 = 5.5\times 10^{-15} m$, $q_2 = 54e$, $r_2 = 6.2\times 10^{-15} m$? Assume the charge is distributed uniformly throughout the volume of each spherical piece and their surfaces are initially in contact and at rest. Ignore the effect of any orbiting electrons.
2.	18 pts.	Two resistors connected in series have an equivalent resistance of $R_s = 800  \Omega$. When they are connected in parallel the equivalent resistance is $R_p = 100 \Omega$. What is the resistance of each resistor?

3.

19 pts.

A charged cloud produces an electrical field in the air near the Earth's surface. A particle of charge $q_1 = -1.0\times 10^{-9} C$ is acted on by a upward, electrostatic force of magnitude $F_1 = 2\times 10^{-6} N$ when placed in this field. a. What is the magnitude and direction of the electric field? b. If the gravitational and electrostatic forces are balanced so the particle does not move up or down, then what is the mass of the particle? c. How many electrons would the particle have to gain or lose to be in this state?

Some useful constants, conversion factors, integrals, and formulas.

Coulomb's Law constant ( $k_e = {1 \over 4\pi\epsilon_0}$)	$8.99\times 10^{9} {N-m^2 \over C^2}$
Electron mass	$9.11\times 10^{-31} kg$
Elementary charge ($e$)	$1.60\times 10^{-19} C$
Proton/Neutron mass	$1.67\times 10^{-27} kg$
Permittivity constant ($\epsilon_0$)	$8.85\times 10^{-12} {kg^2\over N-m^2}$
$\rm 1.0 eV$	$1.6\times 10^{-19} J$
$1  u$	$1.67\times 10^{-27} kg$
Gravitational constant ($G$)	$6.67\times 10^{-11} Nm^2/kg^2$
Acceleration of gravity ($g$)	$9.8 m/s^2$

$$\begin{eqnarray*} \int { dx \over (x^2 + a^2 )^{3/2}} = {x \over a^2(x^2 + a^2)^... ...x+d) \qquad & & x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \ [5pt] \end{eqnarray*}$$

$$\vert\vec F_G\vert = G \frac{m_1 m_2}{r^2} \qquad \vert\vec ... ... r_i^2} \hat r_i \qquad \vert\vec E\vert = \int {dq \over r^2}$$

$$\vert\vec E\vert = k {Q \over r^2} \qquad \vert\vec E\vert =... ...n_0} \qquad \vert\vec E\vert = k {qz \over (z^2 + R^2)^{3/2}}$$

$$W \equiv \int \vec F \cdot d\vec s \qquad \Delta V \equiv {\... ...- \int_A^B \vec E \cdot d\vec s \qquad V = k {q\over r} \qquad$$

$$V = k \sum_n {q_n \over r_n} \qquad V = k \int {dq \over r} ... ...partial y} \qquad E_z = - {\partial V \over \partial z} \qquad$$

$$I \equiv {dQ \over dt} = n e v_d A \qquad V = IR \qquad$$

$$R_{equiv} = \sum R_i \qquad {1 \over R_{equiv}} = \sum {1\over R_i}$$

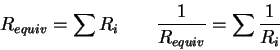
=100000

=2.5in The algebraic sum of the potential changes across all the elements of a closed loop is zero. The sum of the currents entering a junction is equal to the sum of the currents leaving the junction.

$$KE = {1 \over 2}mv^2 \qquad \vec F=m \vec a \qquad ME = KE + PE$$

$$x = \frac{a}{2} t^2 + v_0 t + x_0 \qquad v = at + v_0 \qquad F_g = mg \qquad a_c = \frac{v^2}{r}$$

$${dx^n \over dx} = nx^{n-1} \qquad {d f(u) \over dx} = {df\ov... ... \over dx} f(x)\cdot g(x) = f{dg \over dx} + g{df \over dx}$$