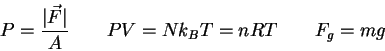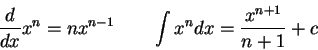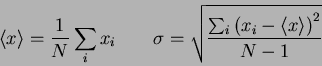Physics 132-1 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Recall the heating curve of a substance as heat is added to it.
If there are regions on the heating curve where the temperature is constant,
what is happening to the added heat in those regions?
- When we measured the latent heat of vaporization of liquid
nitrogen we used a resistor immersed in the liquid as the heat source.
We took some data with the current in the resistor turned off.
Why?
- Boyle's Law states that
 for a gas.
Why should you believe this?
for a gas.
Why should you believe this?
- We measured the specific heat of aluminum
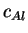 by mixing
a known amount hot (
by mixing
a known amount hot (
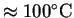 ) aluminum pellets
with a known amount of cold water and recording the final
temperature of the mixture.
The measured values of
) aluminum pellets
with a known amount of cold water and recording the final
temperature of the mixture.
The measured values of 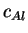 differed from the accepted value
by about 10%.
What are some possible sources of error?
differed from the accepted value
by about 10%.
What are some possible sources of error?
- Recall our analysis of a one-atom gas.
Starting from Newton's Second Law show the force exerted on a wall is
where 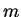 is the mass of the particle,
is the mass of the particle, 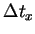 is the time interval
between collisions with the wall, and
is the time interval
between collisions with the wall, and 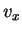 is the component of the velocity
perpendicular to the wall.
Clearly show all steps for full credit.
is the component of the velocity
perpendicular to the wall.
Clearly show all steps for full credit.
- Consider the set of data below which has an average and standard deviation
of
 .
Our theoretical prediction from kinetic theory is
.
Our theoretical prediction from kinetic theory is
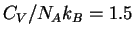 .
Do the data support that prediction?
Why or why not?
Be quantitative in your answer.
.
Do the data support that prediction?
Why or why not?
Be quantitative in your answer.
| Atom |
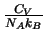 |
| Xe |
1.53 |
| Ar |
1.50 |
| Ne |
1.51 |
| Kr |
1.49 |
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 2. |
17 pts. |
What is the work done by a fluid that expands from
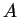 to to 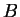 as shown in the figure. as shown in the figure.
![\includegraphics[]{fig1.eps}](img19.png)
|
| 3. |
20 pts. |
What mass of steam at
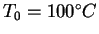 must be mixed
with a mass must be mixed
with a mass  of ice at its melting point in a thermally
insulated container to produce liquid water at of ice at its melting point in a thermally
insulated container to produce liquid water at
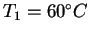 ? ?
|
Some constants.
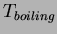 (water) (water) |
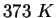 or or
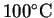 |
 (water) (water) |
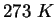 or or 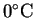 |
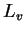 (water) (water) |
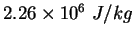 |
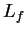 (water) (water) |
 |
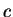 (water) (water) |
 |
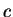 (steam) (steam) |
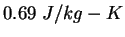 |
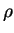 (water) (water) |
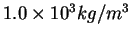 |
 |
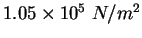 |
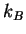 |
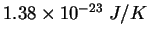 |
proton/neutron mass |
 |
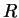 |
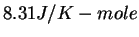 |
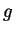 |
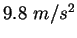 |
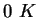 |
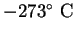 |
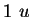 |
 |
| Gravitation constant |
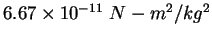 |
Earth's radius |
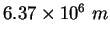 |
Physics 132-3, Study Sheet
Test 1
f 
number of degrees of freedom