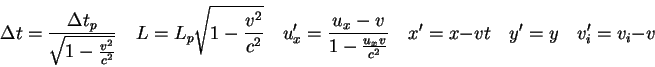![\includegraphics[]{fig1.eps}](img64.png)
![\includegraphics[]{interference.eps}](img65.png)
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (2 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
![\includegraphics[]{fig1.eps}](img64.png)
![\includegraphics[]{interference.eps}](img65.png)
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 8 pts. | An astronaut is traveling in a space vehicle that has a speed
|
| 2. | 8 pts. | A Klingon spaceship moves away from the Earth at a speed
|
| 3. | 8 pts. | When an uncharged conducting sphere of radius 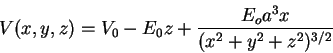
for points outside the sphere, where |
| 4. | 8 pts. | Two moles of an ideal monatomic gas is at an inital temperature
|
| 5. | 10 pts. | A heart surgeon monitors the flow of blood through an artery using
an electromagnetic flowmeter like the one shown in the figure.
The device takes advantage of the presence of ions and electrons in blood as it flows between the poles
of the magnet.
Electrodes
|
| 6. | 10 pts. | One of the dangers of a nuclear explosion is radioactivity
from strontium |
|
Coulomb's Law constant (
|
|
Electron mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Permittivity constant ( |
|
|
|
|
|
|
|
|
|
|
|
Avogadro's number |
|


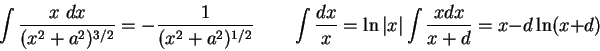
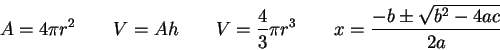
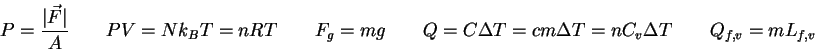
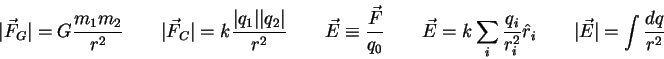
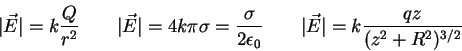
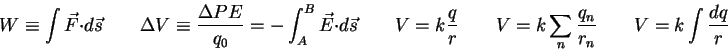
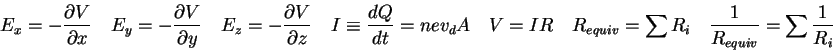
=100000
=2.5in The algebraic sum of the potential changes across all the elements of a closed loop is zero. The sum of the currents entering a junction is equal to the sum of the currents leaving the junction.
![\begin{displaymath}
I = 4 I_0 \cos^2 \left ( {\pi d \over \lambda} \sin \theta \...
... \theta \right )}{\frac{\pi a}{\lambda} \sin \theta}\right ]^2
\end{displaymath}](img61.png)