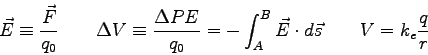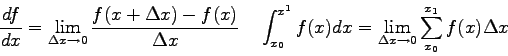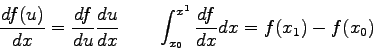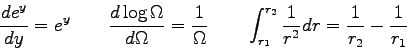Physics 102 Test 3
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Recall the magnetic lines of force we mapped out in lab for a bar magnet.
Does a line of force represent a constant force along its entire length?
Explain.
- Refer to the diagram below. Explain why, at the two points shown on the
circle, the angle between the position vectors
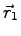 and
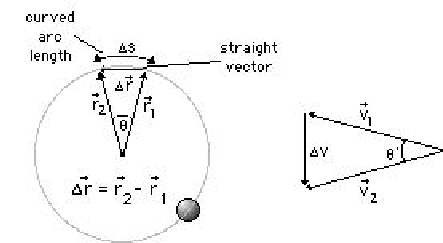
and 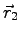 at times
at times 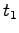 and
and 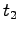 is the same as the angle between the velocity vectors
is the same as the angle between the velocity vectors  and
and 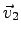 at times
at times 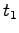 and
and 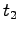 .
.
- Consider the result below from our development of the theory behind the mass spectrometer.
For two particles in a mass spectrometer with the same charge and velocity, but different mass, which one will
have the larger radius?
How will increasing the velocity change the radius?
Explain.
- It is claimed the solution of the differential equation above
describing nuclear decay is the following expression.
Prove this statement by taking the derivative of 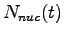 and showing it satisfies the original differential equation which is the following.
and showing it satisfies the original differential equation which is the following.
- Recall the discussion of Newton's corpuscular theory of
light in the laboratory on interference. Does the data you collected for that lab
support Newton's theory or the wave theory?
Why?
- Suppose it could be shown that the cosmic ray intensity at the Earth's surface
was much greater
10,000 years ago.
How would this difference affect what we accept as valid carbon-dated values of
the age of
ancient samples of once-living matter?
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
How many half-lives must elapse until 80% of a radioactive sample of atoms
has decayed?
|
Some constants and conversion factors.
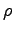 (water) (water) |
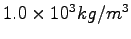 |
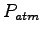 |
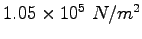 |
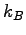 |
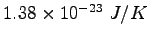 |
Speed of light (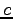 ) ) |
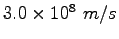 |
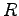 |
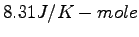 |
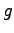 |
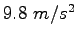 |
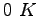 |
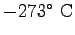 |
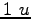 |
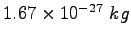 |
Gravitation constant (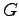 ) ) |
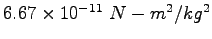 |
Earth's radius |
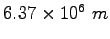 |
Coulomb constant (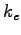 ) ) |
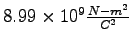 |
Electron mass |
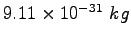 |
Elementary charge (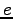 ) ) |
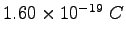 |
Proton/Neutron mass |
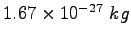 |
Permittivity constant (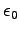 ) ) |
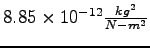 |
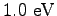 |
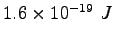 |
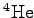 mass mass |
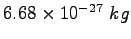 |
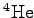 charge charge |
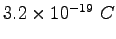 |
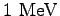 |
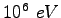 |
|
|
Physics 102 Equations

![]() and showing it satisfies the original differential equation which is the following.
and showing it satisfies the original differential equation which is the following.
![\includegraphics[height=3.0in]{eBfield1.eps}](img23.png)