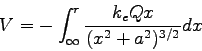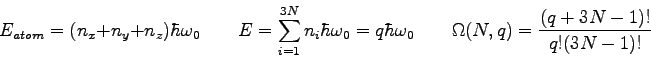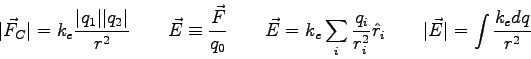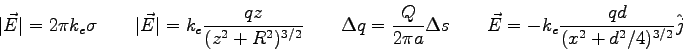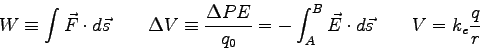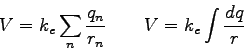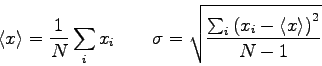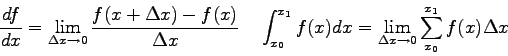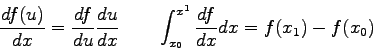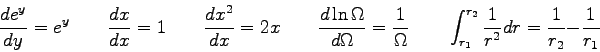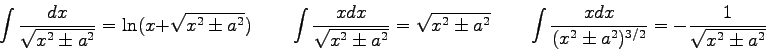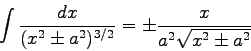Physics 102 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- The plot below shows the entropy for two Einstein solids alone (
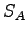 and
and 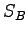 ) and in
contact (
) and in
contact (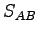 ) as a function of
) as a function of 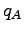 , the number of quanta in Solid
, the number of quanta in Solid 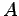 .
What is
.
What is 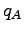 for the most probable macrostate? Mark that point on the plot.
What mathematical condition can you impose
on the total entropy
for the most probable macrostate? Mark that point on the plot.
What mathematical condition can you impose
on the total entropy 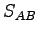 to determine the most probable macrostate?
How are the temperatures of solids
to determine the most probable macrostate?
How are the temperatures of solids 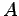 and
and 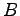 are related at the most probable
microstate?
are related at the most probable
microstate?
![\includegraphics[height=1.75in]{NumberOfStates1.eps}](img71.png)
- Recall the electroscope we used in lab with the thin metal leaf attached
to a post. Suppose you did the following. (1) Rub a rubber rod with wool and bring the
rod near the top of the post of the electroscope, but WITHOUT touching the post with the rod.
(2) Without moving the rod, touch the top of the post with your hand for a few seconds and then remove
your hand. (3) Now remove the rod.
What is the charge, if any, on the electroscope?
Explain your reasoning.
- What do the equipotentials and electric field lines look like between two long, charged plates like the ones in
the figure?
Explain your reasoning.
![\includegraphics[height=0.5in]{plates1.eps}](img72.png)
- Consider our calculation of the electric potential for a ring of charge.
If we calculate
 along the axis of the ring using the known electric field, we
confront the following integral.
along the axis of the ring using the known electric field, we
confront the following integral.
What factors in the integrand can be pulled out in front of the integral?
Explain.
- From Coulomb's Law and the definition of the
electric potential, we expect the spatial variation of the potential
of a point charge
to obey a power law:
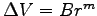 , where
, where 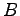 and
and 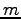 are constants. What do you predict the value of
are constants. What do you predict the value of 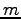 to be?
Why?
to be?
Why?
- A uniform electric field is parallel to the
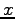 axis.
In what direction can a charge be displaced or moved in this field
without any external work being done of the charge?
Explain.
axis.
In what direction can a charge be displaced or moved in this field
without any external work being done of the charge?
Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
Imagine that the entropy of a certain substance as a function of
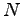 and and 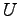 is given by the formula is given by the formula
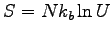 . Using the definition of temperature,
show that the thermal energy of this substance is related to its temperature
by the expression . Using the definition of temperature,
show that the thermal energy of this substance is related to its temperature
by the expression 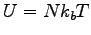 . What is the molar specific heat of the substance? . What is the molar specific heat of the substance?
|
| 2. |
17 pts. |
What are the strength and direction of the electric field at the position
indicated by the dot in terms of 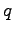 , , 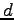 , and any other necessary constants?
Give your answer in component form. , and any other necessary constants?
Give your answer in component form.
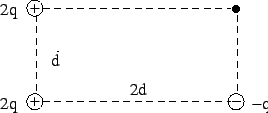
|
| 3. |
20 pts. |
Two large plates with charge density 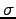 are spaced are spaced
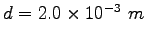 apart
and form a parallel plate capacitor (essentially just two plates that line up with
each other a distance apart
and form a parallel plate capacitor (essentially just two plates that line up with
each other a distance 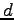 apart).
The electric field between the plates is apart).
The electric field between the plates is
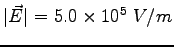 . .
- a.
- What is the expression for the electric field between the plates in terms of
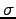 , , 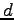 , and any other necessary constants? , and any other necessary constants?
- b.
- Starting from your result for part a, find an expression for the voltage across the plates.
- c.
- What is the voltage across the plates? Calculate a number here.
- c.
- What is the charge density on each disk? Calculate a number here.
|
Some constants and conversion factors.
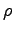 (water) (water) |
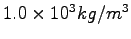 |
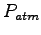 |
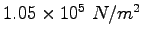 |
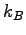 |
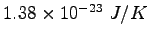 |
Speed of light (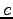 ) ) |
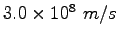 |
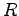 |
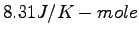 |
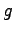 |
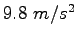 |
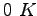 |
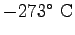 |
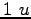 |
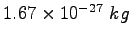 |
Gravitation constant (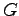 ) ) |
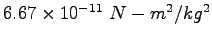 |
Earth's radius |
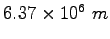 |
Coulomb constant (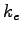 ) ) |
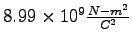 |
Electron mass |
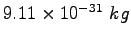 |
Elementary charge (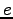 ) ) |
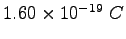 |
Proton/Neutron mass |
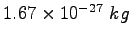 |
Permittivity constant (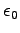 ) ) |
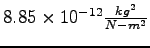 |
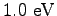 |
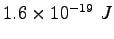 |
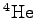 mass mass |
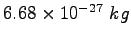 |
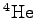 charge charge |
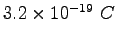 |
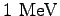 |
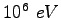 |
|
|
Physics 102 Equations
![\includegraphics[height=1.75in]{NumberOfStates1.eps}](img71.png)
![\includegraphics[height=0.5in]{plates1.eps}](img72.png)
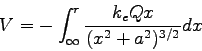
![\includegraphics[height=1.75in]{NumberOfStates1.eps}](img71.png)
![\includegraphics[height=0.5in]{plates1.eps}](img72.png)