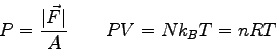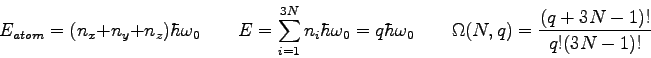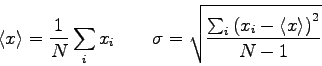Physics 102-1 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Consider a chunk of ice that that is below its freezing point and you start to heat it.
What is the relationship between temperature and added heat after the ice has completely melted,
but before the
water begins to boil?
- A known mass of warm water
 is placed in the calorimeter cup of mass
is placed in the calorimeter cup of mass
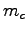 and their
temperature
and their
temperature 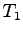 recorded. A known mass of ice
recorded. A known mass of ice 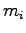 at
at
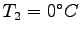 (with
no water) is added to the water and allowed to melt. The final temperature
of the mixture after the ice has melted is
(with
no water) is added to the water and allowed to melt. The final temperature
of the mixture after the ice has melted is 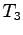 .
What is the complete heat equation in terms of
.
What is the complete heat equation in terms of 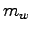 ,
, 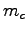 ,
,
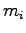 ,
, 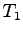 ,
, 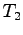 ,
, 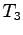 and any known specific heats?
and any known specific heats?
- Consider an ideal gas. If the collisions of the particles of the gas
with the wall perpendicular to the
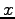 direction
are elastic, show that the average force exerted on that wall for each collision
is
direction
are elastic, show that the average force exerted on that wall for each collision
is
 where
where 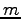 is the mass
of one of the particles and
is the mass
of one of the particles and 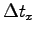 is the mean time interval between
collisions with the wall. Start from Newton's Second
Law.
Clearly show all steps.
is the mean time interval between
collisions with the wall. Start from Newton's Second
Law.
Clearly show all steps.
- We showed that the change in internal energy of a gas is
 |
(1) |
How is
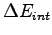 related to the molar specific heat at constant volume
related to the molar specific heat at constant volume  ?
Using your answer and the equation above, show
how
?
Using your answer and the equation above, show
how  is related to Avogadro's number
is related to Avogadro's number 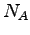 and
and 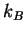 .
.
- Consider the measurements shown in the table below for a test of the
impulse momentum theorem in one dimension where
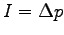 . The average impulse
is
. The average impulse
is
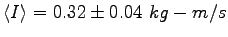 . The average momentum change
is
. The average momentum change
is
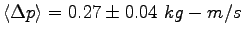 .
Do these data confirm the impulse-momentum theorem? Explain.
.
Do these data confirm the impulse-momentum theorem? Explain.
| Impulse (kg-m/s) |
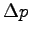 (kg-m/s) (kg-m/s) |
| 0.31 |
0.32 |
| 0.25 |
0.24 |
| 0.34 |
0.30 |
| 0.33 |
0.26 |
- Recall the demonstration where we poured liquid nitrogen on a balloon.
The balloon shrank down so that is was essentially flat and after we ran out of
liquid nitrogen the balloon warmed up and the volume gradually expanded until it was the same
size before we poured nitrogen on it.
Consider the work down by the gas in the balloon when it was warming up.
Was the work positive, negative, or zero? Explain.
If the work was not zero, did this effect increase or decrease the internal
energy of the gas in the balloon?
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
What is the multiplicity of an Einstein solid
with 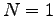 and and
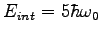 ?
List all the microstates. ?
List all the microstates.
|
Physics 132-2 Equations and Constants
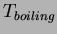 ( (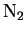 ) ) |
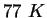 |
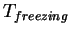 ( (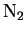 ) ) |
 |
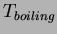 (water) (water) |
 or or
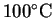 |
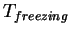 (water) (water) |
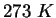 or or  |
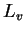 (water) (water) |
 |
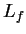 (water) (water) |
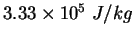 |
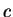 (water) (water) |
 |
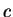 (steam) (steam) |
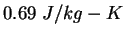 |
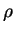 (water) (water) |
 |
 |
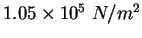 |
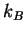 |
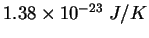 |
proton/neutron mass |
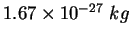 |
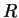 |
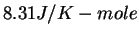 |
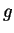 |
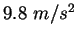 |
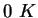 |
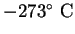 |
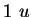 |
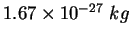 |
| Gravitation constant |
 |
Earth's radius |
 |
f 
number of degrees of freedom