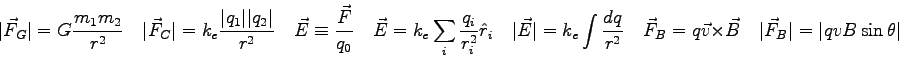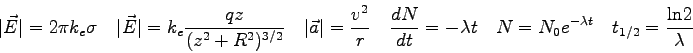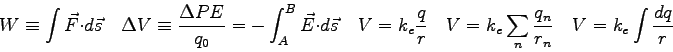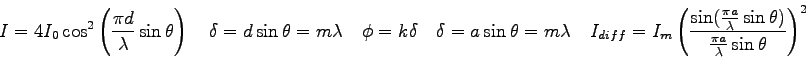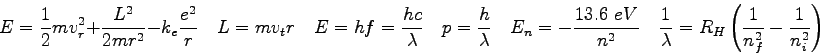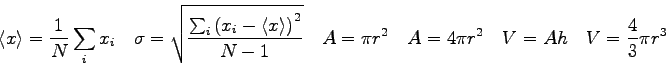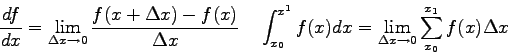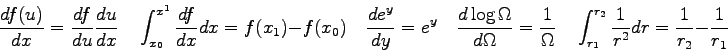Physics 102 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (4 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- One can derive a prediction for the intensity
pattern due to diffraction of light passing through a single slit.
The result is
where  is the size of the single slit,
is the size of the single slit, 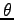 is the angular
position of the phototransistor relative to the incident beam,
is the angular
position of the phototransistor relative to the incident beam, 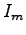 is the maximum intensity at the center of the diffraction pattern,
and
is the maximum intensity at the center of the diffraction pattern,
and 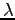 is the wavelength of the light.
The figure below shows the diffraction pattern has a central maximum
with a series of points where the intensity goes to zero at positive
and negative angles. When is the expression for the intensity in the
equation above equal to zero?
is the wavelength of the light.
The figure below shows the diffraction pattern has a central maximum
with a series of points where the intensity goes to zero at positive
and negative angles. When is the expression for the intensity in the
equation above equal to zero?
![\includegraphics[height=1.5in]{diffraction_of_light_fig_3.eps}](img113.png)
- A known mass of water
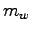 is placed in the calorimeter cup of mass
is placed in the calorimeter cup of mass
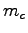 and specific heat
and specific heat  and their
temperature
and their
temperature  recorded.
A known mass of warm metal pellets
recorded.
A known mass of warm metal pellets 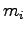 at
at 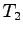 (with unknown specific heat
(with unknown specific heat  ) is added to the water. The final temperature
of the mixture after reaching equilibrium is
) is added to the water. The final temperature
of the mixture after reaching equilibrium is 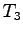 .
What is the complete heat equation in terms of these quantities and any known specific heats?
.
What is the complete heat equation in terms of these quantities and any known specific heats?
- Consider a gas in a container. Would it violate Newton's Laws or any other physical law
if all the particles in the gas collided in such a way that all of the gas particles
ended up in the bottom half of the container leaving the top half empty?
Explain.
- Recall the laboratory on the kinetic theory of ideal gases where you calculated
the specific heat of an ideal gas.
We claimed this calculation supported the atomic theory.
How?
- Is the gravitation constant
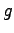 (the acceleration of gravity at the Earth's
surface) really a constant? Explain.
(the acceleration of gravity at the Earth's
surface) really a constant? Explain.
- Find some equipotential surfaces for the charge configuration
shown below, which consists of two charged metal plates placed parallel
to each other. What is the shape of the equipotential surfaces?
Explain your method for finding the equipotentials.
![\includegraphics[height=1.5in]{electric_potential_fig_8.eps}](img114.png)
- The two magnets shown in the figure are identical.
Identify a point on the figure where the magnetic field is
zero. Explain how you picked the point.
![\includegraphics[height=1.25in]{f3.eps}](img115.png)
- Consider an electron entering a uniform magnetic field created by some
Helmholtz coils.
What is the direction of the magnetic force
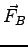 on the negatively charged
electron if
on the negatively charged
electron if
 and
and
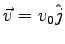 ?
?
- The results for the age of the Shroud of Turin are shown in the table
below for the three labs that performed the measurements.
The typical uncertainty in these measurements is a standard deviation
of
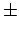 40 years. Are the results of the three laboratories
consistent? Explain.
40 years. Are the results of the three laboratories
consistent? Explain.
| Laboratory |
R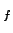 |
Age (years) |
| Arizona |
1.20 x 10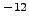 |
662 |
| Oxford |
1.18 x 10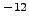 |
801 |
| Zurich |
1.19 x 10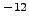 |
731 |
- The position of the interference maxima in a double-slit measurement
can be described by
where 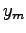 is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and
is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and 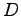 is
the distance from the slits to the phototransistor. The quantity
is
the distance from the slits to the phototransistor. The quantity 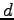 is the slit separation,
is the slit separation, 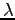 is the wavelength of the light,
and
is the wavelength of the light,
and 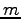 is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
- The hydrogen energy level diagram is shown in the figure.
If a hydrogen atom is in the
 state, it will emit light when it loses
energy and drops down to another energy state.
What state should it jump to in order to emit light with the longest
possible wavelength?
Explain.
state, it will emit light when it loses
energy and drops down to another energy state.
What state should it jump to in order to emit light with the longest
possible wavelength?
Explain.
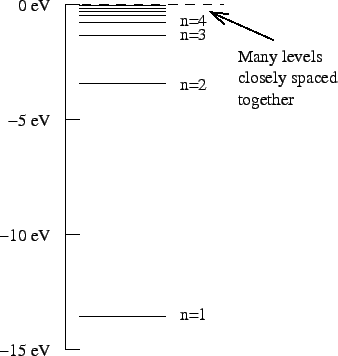
- An airplane flies due west in the northern hemisphere where the Earth's magnetic field
points downward and to the north.
On which wing, left or right, are some of the conduction electrons moved to the wingtip by
the magnetic force on them?
Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
6 pts. |
What are the wavelengths of the first two members of the Lyman
series in the spectrum of hydrogen (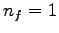 )?
What is the series limit for the Lyman series? )?
What is the series limit for the Lyman series?
|
| 2. |
8 pts. |
You need to use your cell phone which broadcasts a 900 MHz signal, but you're
behind two massive, radio-absorbing buildings that have only a 20 m space between them.
What is the angular width, in degrees, of the electromagnetic wave after it emerges
from between the buildings?
|
Some constants and conversion factors.
 (water) (water) |
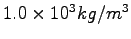 |
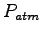 |
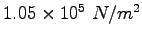 |
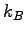 |
 |
Speed of light (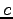 ) ) |
 |
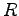 |
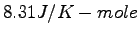 |
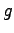 |
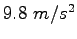 |
 |
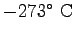 |
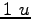 |
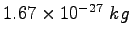 |
Gravitation constant ( ) ) |
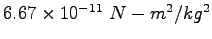 |
Earth's radius |
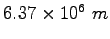 |
Coulomb constant (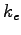 ) ) |
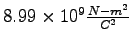 |
Earth's mass |
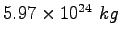 |
Elementary charge (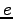 ) ) |
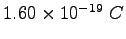 |
Proton/Neutron mass |
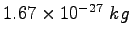 |
Permittivity constant (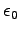 ) ) |
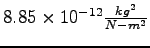 |
Electron mass |
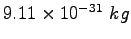 |
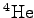 mass mass |
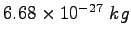 |
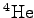 charge charge |
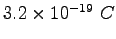 |
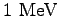 |
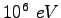 |
 |
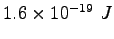 |
Planck's constant (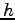 ) ) |
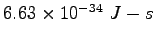 |
Planck's constant (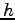 ) ) |
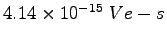 |
Planck's constant (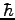 ) ) |
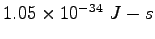 |
Planck's constant (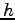 ) ) |
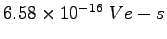 |
Boltzmann's Constant (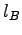 ) ) |
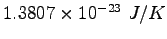 |
Rydberg constant (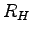 ) ) |
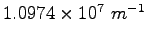 |
Physics 102 Final
f  number of degrees of freedom
number of degrees of freedom
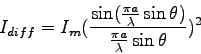
![]() is the size of the single slit,
is the size of the single slit, ![]() is the angular
position of the phototransistor relative to the incident beam,
is the angular
position of the phototransistor relative to the incident beam, ![]() is the maximum intensity at the center of the diffraction pattern,
and
is the maximum intensity at the center of the diffraction pattern,
and ![]() is the wavelength of the light.
The figure below shows the diffraction pattern has a central maximum
with a series of points where the intensity goes to zero at positive
and negative angles. When is the expression for the intensity in the
equation above equal to zero?
is the wavelength of the light.
The figure below shows the diffraction pattern has a central maximum
with a series of points where the intensity goes to zero at positive
and negative angles. When is the expression for the intensity in the
equation above equal to zero?
![\includegraphics[height=1.5in]{diffraction_of_light_fig_3.eps}](img113.png)
![\includegraphics[height=1.5in]{electric_potential_fig_8.eps}](img114.png)
![\includegraphics[height=1.25in]{f3.eps}](img115.png)
![]() is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and
is the distance of a bright spot from the central
maximum (the distance along the slide in this experiment) and ![]() is
the distance from the slits to the phototransistor. The quantity
is
the distance from the slits to the phototransistor. The quantity ![]() is the slit separation,
is the slit separation, ![]() is the wavelength of the light,
and
is the wavelength of the light,
and ![]() is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
is the order of the bright spot. Generate an expression for
the distance between adjacent bright spots.
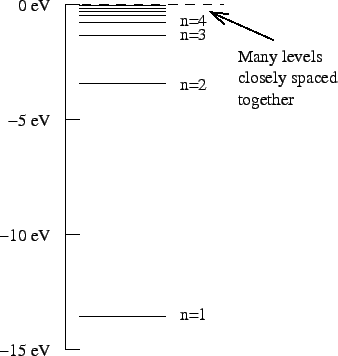
![\includegraphics[height=2.5in]{MassSpec1.eps}](img44.png)
![\includegraphics[height=1.5in]{Efield1.eps}](img51.png)