IQS Physics S2 Test
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Physics Questions (5 pts. apiece) Answer in complete, well-written sentences ONLY WITHIN the spaces provided.
- Recall the laboratory Periodic Motion where you measured the motion of a
harmonic oscillator.
When the mass has its maximum velocity, is its distance from the motion sensor maximum, minimum,
the equilibrium value, or some other value?
- You are on a white horse, riding off at sunset with your beau on a chestnut
mare riding at your side. Your horse has a speed of
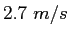 and your beau's
horse has a speed of
and your beau's
horse has a speed of 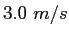 , yet he/she constantly remains at your side. Where
are your horses? Describe the motion. Make a sketch to explain your answer.
, yet he/she constantly remains at your side. Where
are your horses? Describe the motion. Make a sketch to explain your answer.

- Recall the laboratory entitled Newton's Second Law for Rotation where you
applied a torque to a rotator using a pulley and a weight on a string.
What is the formula for the torque on the rotating system as
a function of the magnitude of the hanging mass
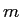 and radius,
and radius, 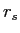 ,
of the spool? Describe each variable in your equation.
,
of the spool? Describe each variable in your equation.
Name:
- A bola consists of three heavy balls connected to a common point by three equal lengths
of sturdy string. It is readied for launch by holding one of the balls overhead and rotating the wrist,
causing the other two balls to rotate in a horizontal circle about the hand. See figure (a) below.
The bola is then released and its configuration rapidly changes from that shown in the overhead
view of the left-hand side of the figure below (a) to the one on the right-hand side (b).
During this change in configuration does the angular speed of the bola about its
center of mass increase, decrease, or stay the same? Explain.
![\includegraphics[width=1.75in]{q4c.ps}](img6.png)
DO NOT WRITE BELOW THIS LINE.
Problems (3). Clearly show all reasoning for full credit.
Show all work on the page below each problem.
See next page.
See next page.
| 3. |
10 pts. |
A hoop of mass 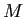 and radius and radius 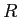 rotates about an axle at the edge of the hoop.
The hoop starts at its highest position and is given a very small push to start it rotating.
At its lowest position, what is the angular velocity of the hoop?
What is the speed of the lowest point on the hoop? rotates about an axle at the edge of the hoop.
The hoop starts at its highest position and is given a very small push to start it rotating.
At its lowest position, what is the angular velocity of the hoop?
What is the speed of the lowest point on the hoop?
![\includegraphics[width=1.75in]{p3b.ps}](img15.png)
|
Physics Constants, Conversion Factors, and Equations
Speed of Light (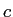 ) ) |
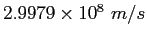 |
proton/neutron mass |
 |
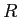 |
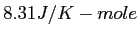 |
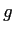 |
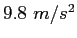 |
| Earth's mass |
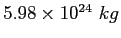 |
Earth's radius |
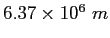 |
| Earth-Moon distance |
 |
Electron mass |
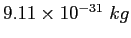 |
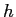 |
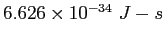 |
 |
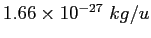 |

![\includegraphics[width=1.75in]{q4c.ps}](img6.png)

![\includegraphics[width=1.75in]{q4c.ps}](img6.png)
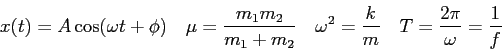
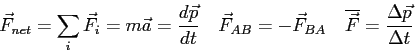
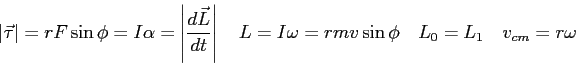
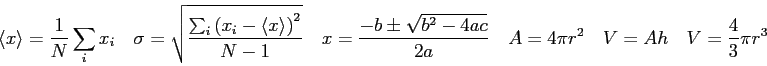
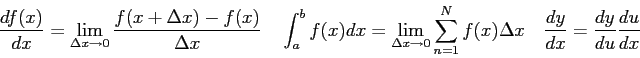
![\includegraphics[width=6.0in]{10t02a2.ps}](img42.png)
![\includegraphics[width=6.0in]{10t02b2.ps}](img43.png)
![\includegraphics[height=9.0in]{periodicChart1.ps}](img44.png)