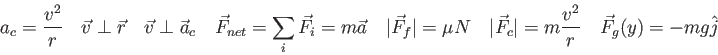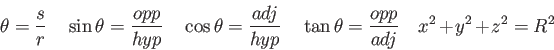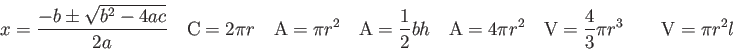IQS Physics F2 Test
Physics Questions (10 pts. apiece) Answer in complete, well-written sentences ONLY WITHIN the spaces provided.
- Recall the laboratory where you measured the position of a cart on a track after you pushed it away from the motion sensor.
Assume the track is tilted upward so the cart is going up after your initial push.
On the graphs below draw your prediction for the position, velocity, and acceleration graphs.
Assume the time axes are all aligned.
![\includegraphics[width=2.50in]{position.eps}](img28.png)
![\includegraphics[width=2.50in]{velocity.eps}](img29.png)
![\includegraphics[width=2.50in]{acceleration.eps}](img30.png)
- In the Force and Motion laboratory you found the acceleration was proportional to the applied force.
What does that say about the meaning of the constant of proportionality?
- Recall the diagram shown below from the circular motion laboratory.
The speed of the object as it rotates around the circle is given by
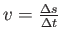 .
Is the change in arc length,
.
Is the change in arc length, 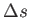 , larger or smaller than the magnitude
of the change in the position vector,
, larger or smaller than the magnitude
of the change in the position vector, 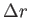 ? Why?
Explain why the arc length
change and the change in the position vector are approximately the same when
? Why?
Explain why the arc length
change and the change in the position vector are approximately the same when
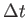 is very small.
is very small.
![\includegraphics[height=5.0cm]{centripetalFig1.eps}](img31.png)
- A ball is projected/thrown horizontally from the top of a building.
One second later another ball is thrown horizontally from the same point and with the
same velocity.
At what point in the motion will the balls be closest together?
Explain.
Ignore air resistance.
Problems (3). Clearly show all reasoning for full credit.
Show all work on the page below each problem.
| 2. |
20 pts. |
A daring ranch hand sitting on a tree limb wants to drop vertically onto a horse galloping under
the tree.
The constant speed of the horse is 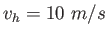 and the vertical distance from the tree limb to the saddle
is and the vertical distance from the tree limb to the saddle
is 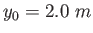 .
What must be the horizontal distance between the limb and the saddle when the ranch hand makes her move? .
What must be the horizontal distance between the limb and the saddle when the ranch hand makes her move?
|
| 3. |
25 pts. |
In a rather interesting experimental procedure an astronaut on the top of a
large mountain on the Moon horizontally launches an experimental package
at high velocity.
What must the be the speed of the package at launch so that it follows a circular orbit and returns to the launch site?
How long does that take?
Assume the acceleration of gravity on the surface of the Moon is one-sixth the value on the Earth.
|
Physics Constants and Equations
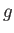 |
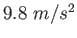 |
proton/neutron mass |
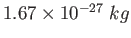 |
| Earth's radius |
 |
Electron mass |
 |
| Moon's radius |
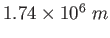 |
Speed of light |
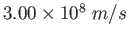 |
![\includegraphics[width=2.50in]{position.eps}](img28.png)
![\includegraphics[width=2.50in]{velocity.eps}](img29.png)
![\includegraphics[width=2.50in]{acceleration.eps}](img30.png)
![\includegraphics[height=5.0cm]{centripetalFig1.eps}](img31.png)
![\includegraphics[width=2.50in]{position.eps}](img28.png)
![\includegraphics[width=2.50in]{velocity.eps}](img29.png)
![\includegraphics[width=2.50in]{acceleration.eps}](img30.png)
![\includegraphics[height=5.0cm]{centripetalFig1.eps}](img31.png)