Physics 131-01 Test 1


I pledge that I have neither given nor received unauthorized assistance during the completion of this work.


Name height0pt depth1pt width2.5in Signature height0pt depth1pt width2.5in


Questions (5 for 8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

$\textstyle \parbox{3.5in}{\item The velocity graph here shows the motion of two... ...is \lq ahead'? Explain. (b) Does either object A or B reverse direction? Explain.}$
Image fig1



  1. Draw the velocity graph for an object whose motion produced the position-time graphs shown below. Position is in meters and velocity in meters per second. Note: Unlike most real objects, you can assume these objects can change velocity so quickly that it looks instantaneous with this time scale. Explain your reasoning.

    Image fig2





  2. If an object's average velocity is zero in some time interval $\Delta t$, what can you conclude (if anything) about the object's displacement during the same time interval? Explain your reasoning.






    DO NOT WRITE ON THIS PAGE BELOW THE LINE.

  3. The figure shows the orientation of the position and velocity vectors for a particle going in a circle with a constant speed `just before' and `just after' the position vector goes through the vertical. How are the angles of the velocity vectors to the horizontal $\theta_1$ and $\theta_2$ related to $\theta_0$? Explain.




  4. The figure shows three situations in which identical projectiles are launched (at the same level) at identical initial speeds and angles. The projectiles do not always land on the same terrain, however. Rank the situations according to the final speeds of the projectiles just before they land, greatest first. Explain your reasoning.

    Image fig4




Problems (3). Clearly show all reasoning for full credit. Use a separate sheet to show your work.

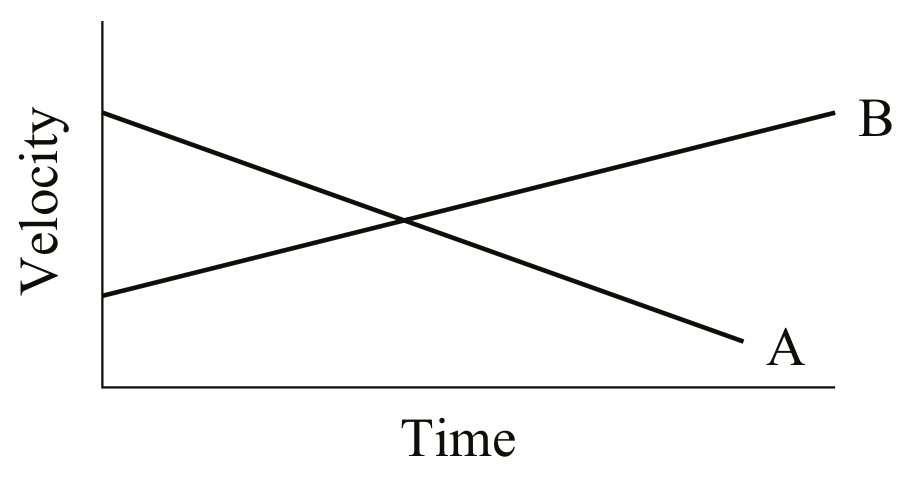
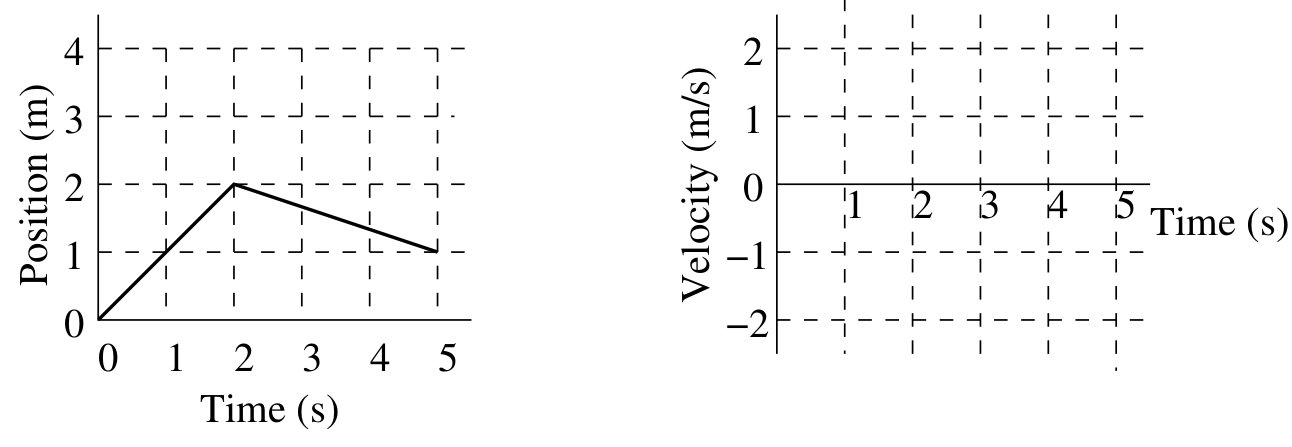
1. 10 pts. The velocity of a particle moving along the $x$ axis is described by

\begin{displaymath} v(t) = At^2 + Bt + C \end{displaymath}

where $t$ is time and $A$, $B$, and $C$ are constants. Evaluate the limit of $\Delta v /\Delta t$ as $\Delta t$ approaches zero. Do NOT use any derivative formulas for specific functions you might remember from calculus.

2. 12 pts. The International Space Station (ISS) is in a circular orbit $4.20\times 10^5 ~ m$ above the Earth's surface, where the free-fall acceleration is $8.56~ m/s^2$. The radius of the Earth is $6.4 \times 10^6 ~ m$. What is the speed of the ISS? What is the time interval required to complete one orbit around the Earth, which is the period of the satellite.

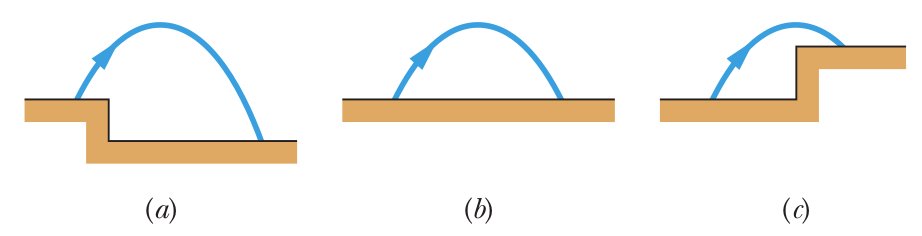
3. 18 pts. A bullet is fired horizontally from a gun with an initial speed $v_i = 500 ~ m/s$ and from an initial height $y_i= 1.5~m$. At the same moment a bullet is dropped from rest and from the same height. What is the time to reach the ground for each object? Assume the ground is flat and ignore the effect of air resistance.

4. 20 pts. The driver of a car hits the brakes when she sees a tree blocking the road ahead. The car skids and slows uniformly with an acceleration of magnitude $5.60~ m/s^2$ for $4.0 ~s$. The skid marks are $70~ m$ long ending at the tree. What is the speed of the car when it strikes the tree?

Physics 131-01 Equations



\begin{displaymath} \Delta x = x_{finish} - x_{start} \qquad \Delta \vec r = \ve... ...{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start} \end{displaymath}


\begin{displaymath} \bar v = \langle v \rangle = {\Delta x \over \Delta t} \quad... ...\to 0} {x (t+\Delta t) - x(t) \over \Delta t} = {dx \over dt} \end{displaymath}


\begin{displaymath} \bar a = \langle a \rangle = {\Delta v \over \Delta t} \quad... ... \to 0} {v(t+\Delta t) - v(t) \over \Delta t} = {dv \over dt} \end{displaymath}


\begin{displaymath} x = {1 \over 2}at^2 + v_it + x_i \qquad v = at + v_i \qquad a_g = -g \end{displaymath}


\begin{displaymath} \vec A = A_x \hat i + A_y \hat j + A_z \hat k \quad \vec A +... ... B = (A_x + B_x)\hat i + (A_y + B_y)\hat i + (A_z + B_z)\hat i \end{displaymath}


\begin{displaymath} a_c = {v^2 \over r} \qquad \vec v_c \perp \vec r_c \qquad \vec v_c \perp \vec a_c \qquad v = \frac{2\pi r}{T} \end{displaymath}


\begin{displaymath} \vec v = {d \vec r \over dt} = {dx \over dt}\hat i + {dy \... ...over dt}\hat i + {dv_y \over dt}\hat j + {dv_z \over dt}\hat k \end{displaymath}


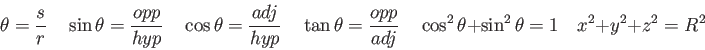
\begin{displaymath} \theta = {s \over r}\quad \sin \theta = {opp \over hyp} \qua... ...uad \cos^2\theta + \sin^2\theta =1 \quad x^2 + y^2 + z^2 = R^2 \end{displaymath}


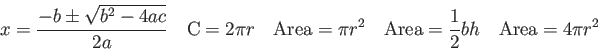
\begin{displaymath} x = {-b \pm \sqrt{b^2 -4ac} \over 2a} \quad {\rm C} = 2 \pi ... ... {\rm Area} = {1 \over 2}bh \quad {\rm Area} = 4 \pi r^2 \quad \end{displaymath}


\begin{displaymath} {\rm Volume} = {4 \over 3} \pi r^3 \quad {\rm Volume} = \pi ... ...sin B}{b} = \frac{\sin C}{c} \quad c^2 = a^2 + b^2 - 2ab\cos C \end{displaymath}



Physics 131-01 Constants

Speed of Light ($c$) $2.9979\times 10^8~m/s$ proton/neutron mass $1.67\times 10^{-27}~kg$
$R$ $8.31J/K-mole$ $g$ $9.8~m/s^2$
Gravitation constant $6.67 \times 10^{-11}~N-m^2/kg^2$ Earth's radius $6.37\times 10^6~m$
Earth-Moon distance $3.84\times 10^8~m$ Electron mass $9.11\times 10^{-31}~kg$