height0pt depth1pt width5.0in
Do not write below this line.

Was the Times' correct and how might you respond?
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

Was the Times' correct and how might you respond?
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 15 pts. | An object in simple harmonic motion
oscillates with a period of
|
| 2. | 20 pts. | A package of mass
|
| 3. | 25 pts. | In the final rescue scene of the movie The Martian
Commander Lewis and Mark Watney are spinning around each other on a tether
of length
|


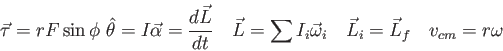
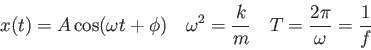

| Speed of Light ( |
|
proton/neutron mass |
|
| Gravitation constant |
|
Earth's radius |
|
| Earth-Moon distance |
|
Electron mass |
|